点击上方“Deephub Imba”,关注公众号,好文章不错过 !
数据是模型的基础,但是没有数据只有领域专家也可以很好地描述或甚至预测给定环境的“情况”。我将根据贝叶斯概率来总结知识驱动模型的概念,然后是一个实际教程,以演示将专家的知识转换为贝叶斯模型以进行推理的步骤。我将使用 Sprinkler 系统从概念上解释过程中的步骤:从知识到模型。最后我将讨论复杂的知识驱动模型的挑战,以及由于质疑和提取知识而可能发生的系统错误。所有示例都是使用 python 的 bnlearn 库创建的。

我们能把专家的知识运用到模型中去吗?
当我们谈论知识时,它不仅仅是描述性的知识和事实。知识也是对某人或某事的熟悉、认识或理解,程序性知识(技能),或熟人知识[1]。
无论拥有什么知识或者想要使用什么知识,要想使用这些知识建立一个计算机辅助知识模型,它都需要以计算机可解释的方式呈现出来。这意味着需要设计一个构建在一系列过程阶段之上的系统。或者换句话说,一个从流程的输出进入下一个流程的输入的流水线管道,并将多个简单管道可以组合成一个复杂的系统。我们可以用一个有节点和边的图来表示这样一个系统。每个节点对应一个变量,每条边表示变量对之间的条件依赖关系。这样我们就可以根据专家的知识定义一个模型,而最好的方法就是使用贝叶斯模型。
要回答我们提出的问题,‘我们能把专家知识运用到模型中吗?‘这取决于将知识表示为图的准确程度,以及你用概率论定理(也就是贝叶斯图模型)将知识粘合在一起的精确度。除此以外可能还是有一些限制。
贝叶斯图模型是创建知识驱动模型的理想选择
机器学习技术的使用已成为在许多领域获得有用结论和进行预测的标准工具包。但是许多模型是数据驱动的,在数据驱动模型中结合专家的知识是不可能也不容易做到。然而,机器学习的一个分支是贝叶斯图模型(又名贝叶斯网络、贝叶斯信念网络、因果概率网络和影响图),可用于将专家知识整合到模型中并进行推理。请参阅下面具有贝叶斯图形模型优点的一些要点,我将在本文中强调这些要点。
- 将领域/专家知识整合到图中是可能的。
- 它有一个模块化的概念。
- 一个复杂的系统是通过组合更简单的部分来构建的。
- 图论提供了直观的高度交互变量集。
- 概率论提供了结合各部分的粘合剂。
要制作贝叶斯图模型,您需要两个成分:1. 有向无环图 (DAG) 和 2. 条件概率表 (CPT)。只有结合起来才能形成专家知识的表示。
贝叶斯图是有向无环图(DAG)
上面已经提到知识可以被表示为一个系统的过程可以看作一个图。在贝叶斯模型的情况下,图被表示为DAG。但DAG到底是什么?首先,它代表有向无环图,是一个具有节点(变量)和有向边的网络(或图)。图1描述了三个变量(X, Y, Z)可以形成的三种独特模式。节点对应于变量X, Y, Z,而有向边(箭头)表示依赖关系或条件分布。网络是无环的,这意味着不允许(反向)循环。
使用DAG,可以通过组合(较简单的)部分来创建复杂的系统。
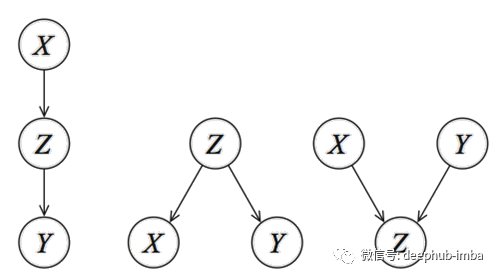
所有DAG(大的或小的)都是根据以下3条规则建造的:
- 边是因果关系。
- 边是有方向性的。
- 不允许有反向循环。
这些规则很重要,因为如果去掉方向性(或箭头),三个dag就会变得相同。换句话说,通过方向性,我们可以使DAG可识别[2]。有许多文章和维基百科页面描述了DAG背后的统计数据和因果关系。每个贝叶斯网络都可以由这三种独特的模式设计并且应该能够代表您想要建模的过程。设计DAG是创建知识驱动模型的第一步。第二部分是定义条件概率表,它用(条件)概率描述每个节点的关系强度。
定义条件概率表来描述节点关系的强度。
概率论(又称贝叶斯定理或贝叶斯规则)是贝叶斯网络的基础。虽然这个定理在这里也适用但有一些不同。首先,在知识驱动模型中,CPT不是从数据中学习的(因为没有数据)。相反,概率需要通过专家的提问得到然后存储在所谓的条件概率表(CPT)(也称为条件概率分布,CPD)中。在本文中,我将交替使用CPT和CPD。
CPT以条件概率或先验来描述每个节点的关系强度。
然后CPT与贝叶斯规则一起使用,以更新允许进行推断的模型信息。在下一节中,我将用例演示如何用专家知识准确地填充CPT。但首先我们介绍下在将专家的知识转化为概率方面存在挑战。
将专家的知识转化为概率
当我们想要创建一个知识驱动的模型时,从专家那里提取正确的信息是至关重要的。领域专家将告知成功过程的概率和副作用的风险,通过这些信息我们可以将风险降到最低。但是当与专家交谈时许多估计的概率都是用语言来表达的,比如“非常有可能”而不是精确的百分比。
我们要做的一项工作就是确保口头概率短语对发送者和接收者在概率或百分比方面是相同的。
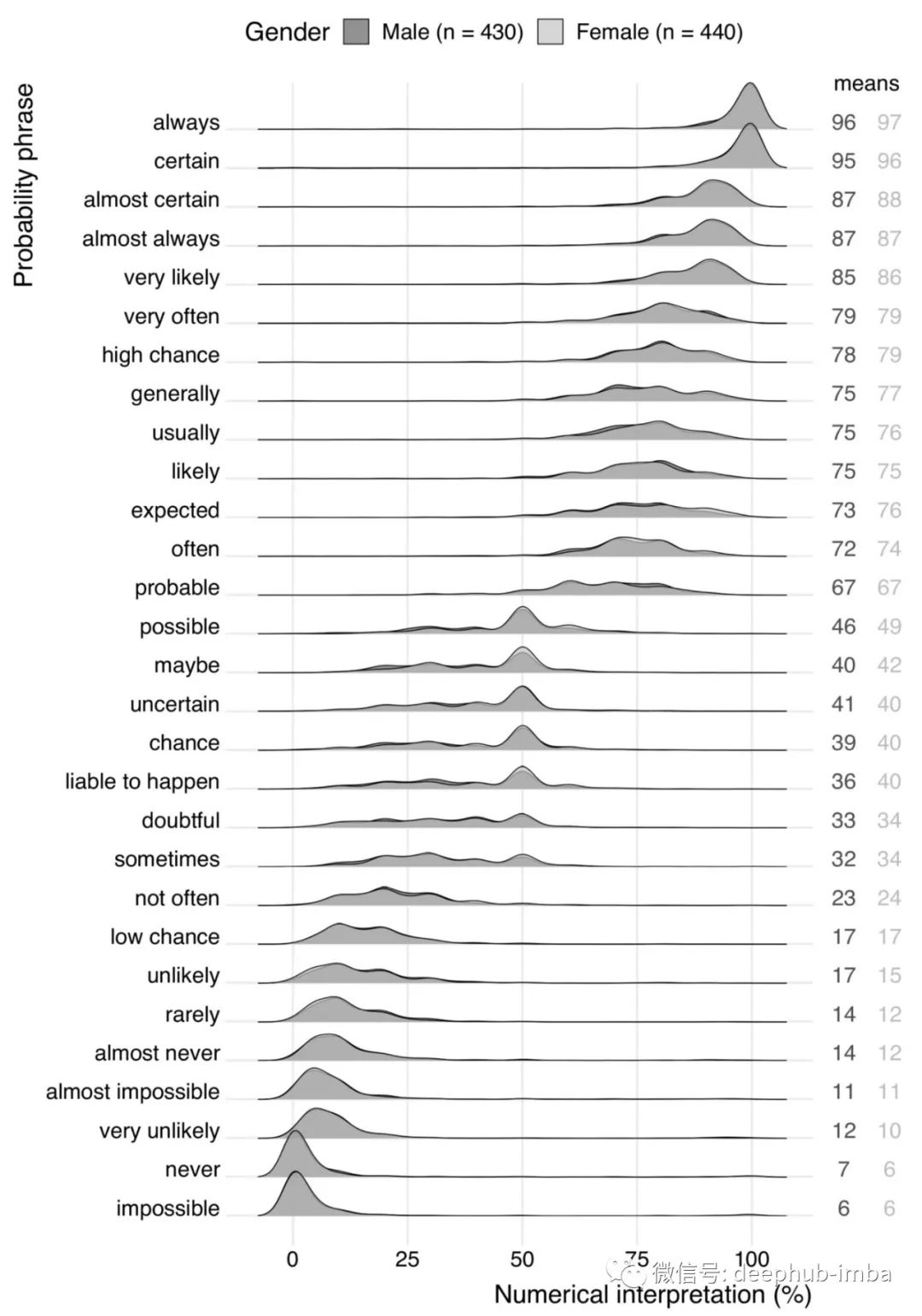
在某些领域,有一些指导方针确定一些常见术语的范围,例如 “常见”的的风险为1-10%。但是,如果没有该领域的背景知识,“常见”这个词很容易被解释为一个不同的数字[4]。此外,概率短语的解释也会受到语境[4]的影响。要小心上下文的误解,因为它也可能导致系统性错误,从而导致错误的模型。概率短语概览图如图2所示。
“不可能”似乎并不总是不可能!
bnlearn 库
关于本文中我们使用bnlearn库。bnlearn 库旨在解决下面的问题:
- 结构学习:给定数据:估计一个捕获变量之间依赖关系的 DAG。
- 参数学习:给定数据和 DAG:估计单个变量的(条件)概率分布。
- 推理:给定学习模型:确定查询的确切概率值。
与其他贝叶斯分析实现相比,bnlearn 有哪些优势?
- 建立在 pgmpy 库之上
- 包含常用的流水线管道操作
- 简单直观
- 开源
根据专家的知识构建系统
让我们从一个简单直观的示例开始演示基于专家知识构建真实世界模型的过程。在这个用例中,我将扮演 洒水 系统领域专家的角色。
假设我的后院有一个洒水系统,在过去的 1000 天里,我亲眼目睹了它的工作方式和时间。我没有收集任何数据,但我对工作产生了一种理论的想法。我们称之为专家观点或领域知识。请注,喷水灭火系统是贝叶斯网络中的一个众所周知的例子。
从我的专家的角度来看,我知道有关该系统的一些事实;它有时开有时关(这是肯定的)。如果洒水系统打开,草 - 可能 - 是湿的。但是,下雨 - 几乎可以肯定 - 也会导致草湿,然后洒水系统 - 大部分时间 - 关闭。我知道在开始下雨之前,云通常会出现。最后,我注意到 洒水系统 和 多云 之间存在弱相互作用,但我不完全确定。
从这一点开始,您需要将专家的知识转换为模型。这可以通过首先创建图然后定义连接图中节点的 CPT 来系统地完成。
洒水系统由四个节点组成,每个节点有两种状态。
洒水系统中有四个节点,可以从专家的角度进行提取。每个节点都有两种状态:雨:是或否,阴天:是或否,洒水系统:开或关,湿草:真或假。
定义简单的一对一关系。
一个复杂的系统都是通过组合更简单的部分来构建的。这意味着不需要立即创建或设计整个系统,而是首先定义更简单的部分。更简单的部分是一对一的关系。在这一步中,我们将把专家的观点转化为关系。我们从专家那里知道:下雨取决于多云状态,湿草取决于雨状态,而湿草也取决于喷水器状态。最后,我们知道洒水取决于阴天。我们可以建立以下四种有向的一对一关系。
多云 → 雨
雨 → 湿草
洒水 → 湿草
多云 → 洒水
重要的是要意识到一对一部分之间的关系强度存在差异,需要使用 CPT 进行定义。但在进入 CPT 之前,让我们首先使用 bnlearn 制作 DAG。
基于一对一关系的DAG
这四个有向关系现在可以用来构建带有节点和边的图来表示。每个节点对应一个变量,每条边表示变量对之间的条件依赖关系。在bnlearn中,我们可以把变量之间的关系赋值并用图形表示出来。
import bnlearn as bn
# Define the causal dependencies based on your expert/domain knowledge.
# Left is the source, and right is the target node.
edges = [('Cloudy', 'Sprinkler'),
('Cloudy', 'Rain'),
('Sprinkler', 'Wet_Grass'),
('Rain', 'Wet_Grass')]
# Create the DAG
DAG = bn.make_DAG(edges)
# Plot the DAG (static)
bn.plot(DAG)
# Plot the DAG (interactive)
bn.plot(DAG, interactive=True)
# DAG is stored in an adjacency matrix
DAG["adjmat"]
下面的图最终的DAG。我们称其为因果DAG,因为我们假设我们编码的边代表了我们对洒水系统的因果假设。
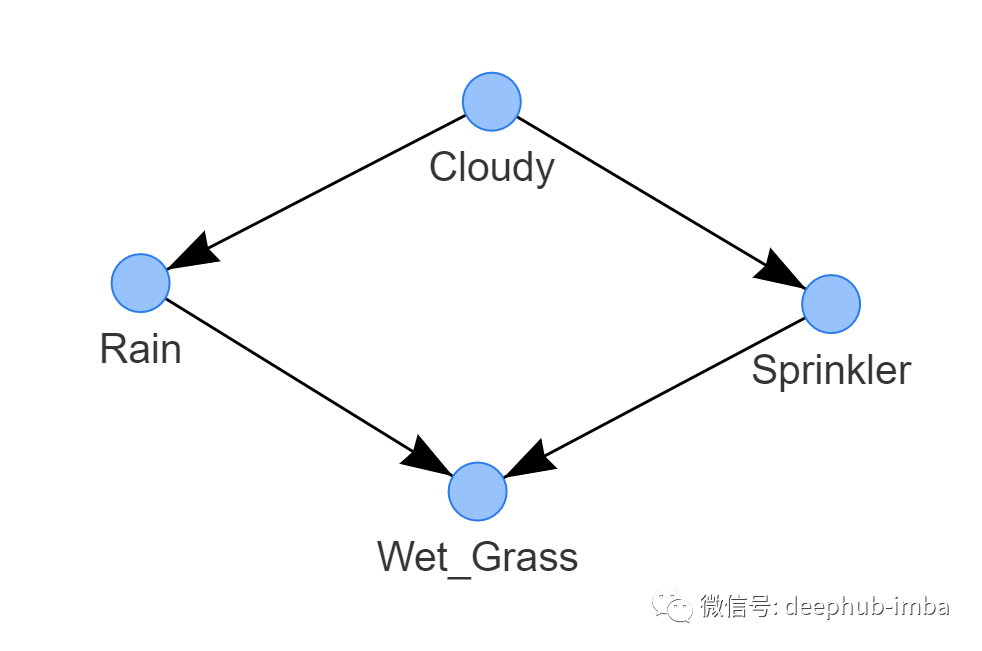
此时,DAG还不知道底层的依赖关系。我们可以用bn.print(DAG)检查cpt,结果是“no CPD can be print”。我们需要用所谓的条件概率表(cpt)向DAG中添加知识,我们将依靠专家的知识来填充cpt。
知识可以通过条件概率表(cpt)添加到DAG中。
建立条件概率表
该洒水系统是一个简单的贝叶斯网络,其中Wet grass(子节点)受双亲节点(Rain和sprinkler)的影响(见图1)。多云。Cloudy节点不受任何其他节点的影响。
我们需要将每个节点与一个概率函数关联起来,该函数以该节点的父变量的一组特定值作为输入,并给出(作为输出)该节点所表示的变量的概率。我们来计算这四个节点。
CPT:Cloudy
Cloudy节点有两种状态(yes或no),并且没有依赖关系。当使用单个随机变量时,计算概率是相对简单的。从我的专家角度来看,在过去1000天里,我亲眼目睹了70%的多云天气。因为概率加起来应该是1,非多云的概率应该是30%。CPT如下所示:
# Import the library
from pgmpy.factors.discrete import TabularCPD
# Cloudy
cpt_cloudy = TabularCPD(variable='Cloudy', variable_card=2, values=[[0.3], [0.7]])
print(cpt_cloudy)
+-----------+-----+
| Cloudy(0) | 0.3 |
+-----------+-----+
| Cloudy(1) | 0.7 |
+-----------+-----+
CPT:Rain
Rain节点有两种状态,并且以Cloudy为条件,Cloudy也有两种状态。总的来说,我们需要指定4个条件概率,即一个事件发生时另一个事件发生的概率。在我们的例子中,在多云的情况下下雨的概率。因此,证据是多云,变量是雨。从我的专家的观点来看,下雨的时候,80%的时间也是多云的。我也有20%的时间看到下雨,没有可见的云。
cpt_rain = TabularCPD(variable='Rain', variable_card=2,
values=[[0.8, 0.2],
[0.2, 0.8]],
evidence=['Cloudy'], evidence_card=[2])
print(cpt_rain)
+---------+-----------+-----------+
| Cloudy | Cloudy(0) | Cloudy(1) |
+---------+-----------+-----------+
| Rain(0) | 0.8 | 0.2 |
+---------+-----------+-----------+
| Rain(1) | 0.2 | 0.8 |
+---------+-----------+-----------+
CPT:Sprinkler
Sprinkler节点有两种状态,并受多云两种状态的制约。总的来说,我们需要指定4个条件概率。这里我们需要定义在多云发生的情况下喷头的概率。因此,证据是多云,变量是雨。我能看出来,当洒水器关闭时,90%的时间都是多云的。因此Sprinkler 为 true 且 Cloudy 为 true 的对应值为 10%。其他概率我不确定,所以我将其设置为 50% 的时间。
cpt_sprinkler = TabularCPD(variable='Sprinkler', variable_card=2,
values=[[0.5, 0.9],
[0.5, 0.1]],
evidence=['Cloudy'], evidence_card=[2])
print(cpt_sprinkler)
+--------------+-----------+-----------+
| Cloudy | Cloudy(0) | Cloudy(1) |
+--------------+-----------+-----------+
| Sprinkler(0) | 0.5 | 0.9 |
+--------------+-----------+-----------+
| Sprinkler(1) | 0.5 | 0.1 |
+--------------+-----------+-----------+
CPT:wet grass
wet grass节点有两种状态,受两个父节点制约;雨和洒水器。这里我们需要定义给定雨和洒水器发生湿草的概率。总的来说,我们必须指定 8 个条件概率(2 个状态 ^ 3 个节点)。
作为专家我敢肯定,99%的人在下雨或洒水后看到湿草:P(wet grass=1 | rain=1, sprinkler =1) = 0.99。因此对应的P(wet grass=0|rain=1,sprinkler =1)=1 - 0.99 = 0.01
作为专家我完全肯定,没有下雨或者没有开洒水器的时候草不会湿:P(wet grass=0 | rain=0,sprinkler =0)= 1。对应的是:P(wet grass=1 |rain=0,sprinkler =0)=1 - 1= 0
作为专家我知道,湿草几乎总是发生在下雨的时候,当洒水器关闭(90%)。P(wet grass=1 | rain=1,sprinkler =0)= 0.9。对应的是:P(wet grass=0 | rain=1,sprinkler =0)=1 - 0.9 = 0.1。
作为专家我知道,草湿了并且不下雨的时候,洒水器总是开着(90%)。P(wet grass=1 | rain=0,sprinkler =1)= 0.9。对应的是:P(wet grass=0 | rain=0,sprinkler =1)=1 - 0.9 = 0.1。
cpt_wet_grass = TabularCPD(variable='Wet_Grass', variable_card=2,
values=[[1, 0.1, 0.1, 0.01],
[0, 0.9, 0.9, 0.99]],
evidence=['Sprinkler', 'Rain'],
evidence_card=[2, 2])
print(cpt_wet_grass)
+--------------+--------------+--------------+--------------+--------------+
| Sprinkler | Sprinkler(0) | Sprinkler(0) | Sprinkler(1) | Sprinkler(1) |
+--------------+--------------+--------------+--------------+--------------+
| Rain | Rain(0) | Rain(1) | Rain(0) | Rain(1) |
+--------------+--------------+--------------+--------------+--------------+
| Wet_Grass(0) | 1.0 | 0.1 | 0.1 | 0.01 |
+--------------+--------------+--------------+--------------+--------------+
| Wet_Grass(1) | 0.0 | 0.9 | 0.9 | 0.99 |
+--------------+--------------+--------------+--------------+--------------+
我们定义了DAG中与cpt之间关系的强度。现在我们需要连接DAG和cpt。
用CPT更新DAG:
所有CPT都创建好了,我们现在可以将它们与DAG连接。作为完整性检查可以使用print_DAG功能检查cpt。
# Update DAG with the CPTs
model = bn.make_DAG(DAG, CPD=[cpt_cloudy, cpt_sprinkler, cpt_rain, cpt_wet_grass])
# Print the CPTs
bn.print_CPD(model)
"""
[bnlearn] >No changes made to existing Bayesian DAG.
[bnlearn] >Add CPD: Cloudy
[bnlearn] >Add CPD: Sprinkler
[bnlearn] >Add CPD: Rain
[bnlearn] >Add CPD: Wet_Grass
[bnlearn] >Checking CPDs..
[bnlearn] >Check for DAG structure. Correct: True
CPD of Cloudy:
+-----------+-----+
| Cloudy(0) | 0.3 |
+-----------+-----+
| Cloudy(1) | 0.7 |
+-----------+-----+
CPD of Sprinkler:
+--------------+-----------+-----------+
| Cloudy | Cloudy(0) | Cloudy(1) |
+--------------+-----------+-----------+
| Sprinkler(0) | 0.5 | 0.9 |
+--------------+-----------+-----------+
| Sprinkler(1) | 0.5 | 0.1 |
+--------------+-----------+-----------+
CPD of Rain:
+---------+-----------+-----------+
| Cloudy | Cloudy(0) | Cloudy(1) |
+---------+-----------+-----------+
| Rain(0) | 0.8 | 0.2 |
+---------+-----------+-----------+
| Rain(1) | 0.2 | 0.8 |
+---------+-----------+-----------+
CPD of Wet_Grass:
+--------------+--------------+--------------+--------------+--------------+
| Sprinkler | Sprinkler(0) | Sprinkler(0) | Sprinkler(1) | Sprinkler(1) |
+--------------+--------------+--------------+--------------+--------------+
| Rain | Rain(0) | Rain(1) | Rain(0) | Rain(1) |
+--------------+--------------+--------------+--------------+--------------+
| Wet_Grass(0) | 1.0 | 0.1 | 0.1 | 0.01 |
+--------------+--------------+--------------+--------------+--------------+
| Wet_Grass(1) | 0.0 | 0.9 | 0.9 | 0.99 |
+--------------+--------------+--------------+--------------+--------------+
[bnlearn] >Independencies:
(Wet_Grass ⟂ Cloudy | Rain, Sprinkler)
(Rain ⟂ Sprinkler | Cloudy)
(Cloudy ⟂ Wet_Grass | Rain, Sprinkler)
(Sprinkler ⟂ Rain | Cloudy)
[bnlearn] >Nodes: ['Cloudy', 'Sprinkler', 'Rain', 'Wet_Grass']
[bnlearn] >Edges: [('Cloudy', 'Sprinkler'), ('Cloudy', 'Rain'), ('Sprinkler', 'Wet_Grass'), ('Rain', 'Wet_Grass')]
"""
带有cpt的DAG如下图所示。
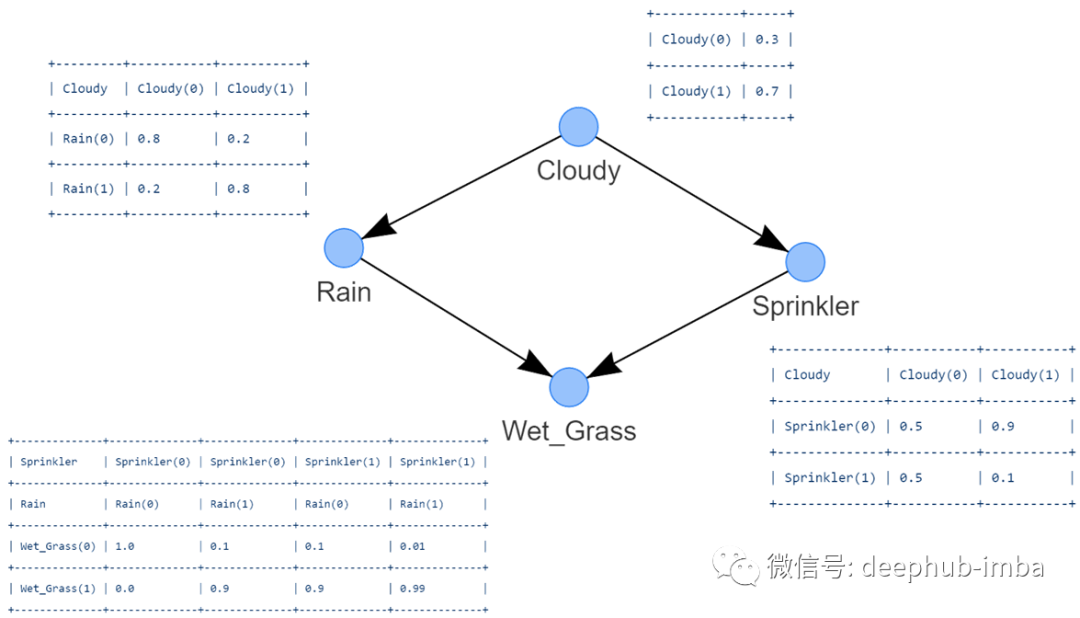
使用因果模型进行推理
我们已经创建了一个描述数据结构的模型,以及定量描述每个节点及其父节点之间的统计关系的cpt。让我们向我们的模型提出一些问题并做出推论!
在洒水器关闭的情况下,草地湿润的可能性有多大?
P(Wet_grass=1 |Sprinkler=0)= 0.6162
如果洒器停了并且天气是多云的,下雨的可能性有多大?
P(Rain=1 |Sprinkler=0,Cloudy=1)= 0.8
import bnlearn as bn
# Make inference on wet grass given sprinkler is off
q1 = bn.inference.fit(model, variables=['Wet_Grass'], evidence={'Sprinkler':0})
print(q1.df)
"""
+--------------+------------------+
| Wet_Grass | phi(Wet_Grass) |
+==============+==================+
| Wet_Grass(0) | 0.3838 |
+--------------+------------------+
| Wet_Grass(1) | 0.6162 |
+--------------+------------------+
"""
# Make inference on Rain, given sprinkler is off and cloudy is true
q2 = bn.inference.fit(model, variables=['Rain'], evidence={'Sprinkler':0, 'Cloudy':1})
print(q2.df)
"""
+---------+-------------+
| Rain | phi(Rain) |
+=========+=============+
| Rain(0) | 0.2000 |
+---------+-------------+
| Rain(1) | 0.8000 |
+---------+-------------+
"""
# Inferences with two or more variables can also be made such as:
q3 = bn.inference.fit(model, variables=['Wet_Grass','Rain'], evidence={'Sprinkler':1})
print(q3.df)
"""
+---------+--------------+-----------------------+
| Rain | Wet_Grass | phi(Rain,Wet_Grass) |
+=========+==============+=======================+
| Rain(0) | Wet_Grass(0) | 0.0609 |
+---------+--------------+-----------------------+
| Rain(0) | Wet_Grass(1) | 0.5482 |
+---------+--------------+-----------------------+
| Rain(1) | Wet_Grass(0) | 0.0039 |
+---------+--------------+-----------------------+
| Rain(1) | Wet_Grass(1) | 0.3870 |
+---------+--------------+-----------------------+
"""
总结
贝叶斯网络的一个优点是,对人类来说直接依赖和局部分布比完整的联合分布更容易直观地理解。为了创造知识驱动的模型,我们需要两个要素;DAG和条件概率表(cpt)。两者都是由专家提问得出的。DAG描述数据的结构,cpt用于定量描述每个节点及其父节点之间的统计关系。尽管这种方法似乎是合理的,但通过询问专家可能出现的系统性错误,以及在构建复杂模型时的局限性。
我怎么知道我的因果模型是正确的?
在洒水器的例子中,我们通过个人经验提取领域专家的知识。虽然我们创建了一个因果关系图,但是很难完全验证因果关系图的有效性和完整性。例如,你可能对概率和图表有不同的看法并且是对的。举个例子,我这样描述:“我在20%的时间里确实看到了雨,没有可见的云。”对这样一种说法进行争论可能是合理的。相反,也可能同时存在多个真实的知识模型。在这种情况下,您可能需要组合这些概率,或者决定谁是正确的。
所使用的知识和专家的经验一样丰富并且和专家一样的带有偏见
换句话说,我们通过询问专家得到的概率是主观概率[5]。在洒水车的例子中,我们可以接受概率的概念是个人的,它反映了一个人在特定时间,特定地点的信念程度。如果专家生活在非洲而不是英国,模型会改变吗?
如果您想使用这样一个过程来设计一个知识驱动的模型,那么了解人们(专家)如何得到概率估计是很重要的。在文献中,人们在对不确定事件进行推理时,很少遵循概率原则,而是用有限的启发式[6,7],如代表性、可得性,来替代概率定律。这可能导致系统性错误,并在一定程度上导致错误的模型。此外,要确保在准确的概率或百分比,对发送者和接收者来说,是需要统一描述的口径的。
复杂性是主要的限制。
本文提出的洒水系统只有几个节点,但贝叶斯网络可以包含更多的节点,并具有多层次的父子依赖关系。在贝叶斯网络中填充条件概率表(CPT)所需的概率分布的数量,随着与该表相关联的父节点的数量呈指数增长。如果该表是通过从领域专家那里获得的知识来填充的,那么任务的规模会形成相当大的认知障碍[8]。
对于领域专家来说,过多的亲子依赖会形成相当大的认知障碍。
例如,如果m个父节点表示布尔变量,那么概率函数就由一个2^m项的表表示,每个可能的父节点组合都有一个项。对于创建大型图(超过10-15个节点)就会非常麻烦,因为父子依赖关系的数量可能会对领域专家构成相当大的认知障碍。如果您有想要建模的系统的数据,还可以使用结构学习[3]来学习结构(DAG)和/或其参数(cpt)。
我们能把专家知识运用到模型中去吗?
我将重复我之前的陈述:“这取决于你用图表表达知识的精确度,以及你用概率论将它们粘合在一起的精确度。”
最后总结
创建一个知识驱动的模型并不容易。它不仅是关于数据建模,而且是关于人类心理。一定要为专家讨论做好准备。多次短沟通比一次长沟通要好。有系统地问问题:首先设计具有节点和边的图,然后进入cpt。在讨论可能性时要谨慎。了解专家如何得出他的概率并在需要时进行标准化。检查时间和地点是否会导致不同的结果。在构建模型之后进行完整性检查。
引用
- Wikipedia, Knowledge
- Pearl, Judea (2000). Causality: Models, Reasoning, and Inference. Cambridge University Press. ISBN 978 – 0 – 521 – 77362 – 1. OCLC 42291253.
- E.Taskesen, A Step-by-Step Guide in detecting causal relationships using Bayesian Structure Learning in Python, Medium, 2021
- Sanne Willems, et al, Variability in the interpretation of probability phrases used in Dutch news articles — a risk for miscommunication, JCOM, 24 March 2020
- R. Jeffrey, Subjective Probability: The Real Thing, Cambridge University Press, Cambridge, UK, 2004.
- A. Tversky and D. Kahneman, Judgment under Uncertainty: Heuristics and Biases, Science, 1974
- Tversky, and D. Kahneman, ‘Judgment under uncertainty: Heuristics and biases,’ in Judgment under Uncertainty: Heuristics and Biases, D. Kahneman, P. Slovic, and A. Tversky, eds., Cambridge University Press, Cambridge, 1982, pp 3–2
- Balaram Das, Generating Conditional Probabilities for Bayesian Networks: Easing the Knowledge Acquisition Problem. Arxiv
作者:Erdogan Taskesen
喜欢就关注一下吧:
点个 在看 你最好看!********** **********