密码编码学与网络安全(第五版)课后习题-CH03

思考题（部分）

3.1 为什么说研究Feistel密码很重要？

feistel 是使用乘积密码获得简单的代换密码，乘积密码指的是执行两个或多个基本的密码系统，最后的密码强度要高于每个基本密码系统产生的结果

3.2 分组密码和流密码的差别是什么?

分组密码是每次处理输入的一组元素，相应的得到一组密文元素。流密码则是连续的处理输入元素，每次输出一个密文元素。也就是说流密码是一个比特w个比特的加密，分组密码是若干比特(定长)同时加密。比如des是64比特的明文一次性加密成密文。

密码分析方面有很多不同。比如流密码中，比特流的很多统计特性影响到算法的安全性。

密码实现方面有很多不同。比如流密码通常是在特定硬件设备上实现。分组密码既可以在硬件实现，也方便在计算机上软件实现。

3.5 混淆与扩散的差别是什么?

扩散(diffusion):将明文的统计特性散布到密文中去，实现方式是使得明文的每一位影响密文中多位的值，使得每一字母在密文中出现的频率比在明文中出现的频率更接近于相等。其目的是使明文和密文之间的统计关系变得尽可能复杂，使敌手无法得到密钥。

混淆(confusion): 其目的在于使作用于明文的密钥和密文之间的关系复杂化，是明文和密文之间、密文和密钥之间的统计相关特性极小化，从而使统计分析攻击不能奏效。

3.6哪些参数与设计选择决定了Feister 密码的实际算法?

分组长度: 分组越长则安全性越高，但加/解密速度越低，分组长度为64位是一个合理的折衷。

密钥长度: 密钥越长越安全，但加/解密速度越低，64 位长的密钥已被证明是不安全的，128 位是常用的长度

迭代次数: 迭代越多越安全，通常为16次迭代

子密钥产生算法: 越复杂则密码分析越困难

轮函数: 越复杂则抗密码分析的能力越强

3.7 设计DES-S盒的目的是什么？

每个s盒将6位输入变成4位输入，是非线性的，决定了DES算法的安全性

3.9差分密码分析与线性密码分析的区别是什么?

线性密码分析是一种已知明文攻击，也是一种统计攻击，它以求线性近似为基础。通过寻找现代密码算法变换的线性近似来攻击。

差分密码分析的基本思想是:通过分析明文对的差值与密文对的差值的影响来恢复某些密钥位。差分密码分析可用来攻击任何由迭代一个固定的轮函数的结构的密码。

差分密码分析在许多方面与线性密码分析相似,主要区别在于差分密码分析包含了将两个输入的异或与其相对应的两个输出的异或相比较。

习题

3.1 (a)在3.1节的名为“Feistel密码结构设计动机"的小节中说到,对于n位的分组长度,理想分组密
码的不同可逆映射个数为 $2^{n} !$ 个。请证明。

（a）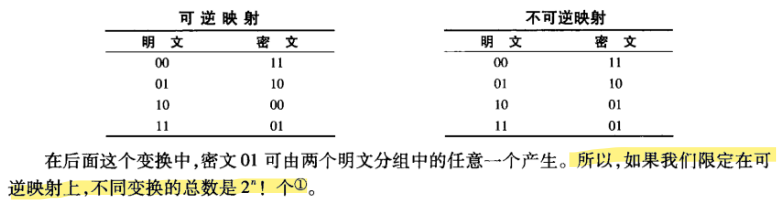

对于一个n-bit的分组长度，存在 $2^{n}$ 大小的密文空间和明文空间，对于可逆映射，每一个不同的明文都要映射唯一的密文，对于第一个明文，我们可以选择 $2^{n}$ 密文中的任意一个，对于第二个明文，我们可以选择剩下 $2^{n}$ - 1密文中的任意一个。以此类推，这种可逆映射个数为 $2^{n} !$

3.1 (b)在同样的小节里说到,对于理想分组密码,若允许所有可逆映射,则密钥的长度为 $n2^{n^{^{}}}$ 位。但
是,如果有 $2^{n}$ !个映射,则应该需要 $\log 2^{n} !$ 个位就可以区分这 $2^{n}$ **!个映射。所以密钥长度应为
** $\log 2^{n} !$ 。然而, $\log 2^{n} !$ < $n2^{n^{^{}}}$ 。请解释这种差别。

理论上，秘钥长度可以是**** $\log 2^{n} !$ 位。我们将 $2^{n} !$ 个映射用整数1开始标记到 $2^{n} !$ ，那么我们只需要建立一个表格，这样利用 $\log 2^{n} !$ -bit长的密钥就可以对应 $2^{\log 2^{n}!} = 2^{n}!$ 种情况。但是同时我们也需要维护这个占用了巨额空间的表格来支撑这个 $\log 2^{n} !$ -****bit的密钥进行映射检索。

由于feistel类的密码解密区别只在于子密钥的使用顺序，而题目给出的子密钥严格对称，所以加密算法和解密算法并没有区别，将拥有的密文c当作明文交给oracle进行加密操作，获得的密文也就是解密后的明文m。（此处可能有人会疑惑，既然加解密的区别只在子密钥使用顺序，为何对称的子密钥加密后不会直接解密【即前8个子密钥加密，后8个子密钥解密】，原因在于在一次迭代的过程中，迭代结尾还有一次左右密文组互换的操作，而算法计算过程中并未在第8个密钥加密后进行互换操作。对于互换操作，我的个人认识是为了方便算法程序的实现，仔细查看文章图3.3会发现，虽然加解密算法上没有区别，但其left和right是相反的，交换操作可以使得算法实现的时候更加方便，只设计一个算法，如果个人认识错误还请指出，谢谢）。

我们只需要考虑剩下N-t的明密文对不一致的情况，即 $1-\frac{1}{(N-t)!}$ .

没看懂题目要干嘛。

这是一种错排问题，这里不使用公式，而用容斥原理解释方便理解。我们设N= $2^{n}$ .则映射共有N!种，其中第i位上是i的映射有C(N,1)(N-1)! = N!/1!种，由于是求没有不动点的映射的可能性，我们应该减去这些排列,同时这样多减了一次两个点为不动点的情况，故在加上C(N,2)(N-2)! = N!/2!种。以此类推，没有不动点的映射种类数是：

    ![N! -\frac{N!}{1!} + \frac{N!}{2!} - \frac{N!}{3!} ... \frac{(-1)^{N}N!}{N!} = N!\sum_{k=2}^{N}\frac{(-1)^{k}}{k!} = \frac{N!}{e}](https://latex.codecogs.com/gif.latex?N%21%20-%5Cfrac%7BN%21%7D%7B1%21%7D%20&amp;plus;%20%5Cfrac%7BN%21%7D%7B2%21%7D%20-%20%5Cfrac%7BN%21%7D%7B3%21%7D%20...%20%5Cfrac%7B%28-1%29%5E%7BN%7DN%21%7D%7BN%21%7D%20%3D%20N%21%5Csum_%7Bk%3D2%7D%5E%7BN%7D%5Cfrac%7B%28-1%29%5E%7Bk%7D%7D%7Bk%21%7D%20%3D%20%5Cfrac%7BN%21%7D%7Be%7D)

所以没有不动点的映射概率为:

$\frac{N!}{e}/N! = \frac{1}{e} \approx 36.8%$

则可以得知多于60%的映射至少有一个不动点

** 3.5 - 3.7 自己想象 3.8自行看书**

首先将TDi和Ti的定义准备好(其实是一样的)：

    ![T_{i} (L||R) = R||L \oplus f(R,K)](https://latex.codecogs.com/gif.latex?T_%7Bi%7D%20%28L%7C%7CR%29%20%3D%20R%7C%7CL%20%5Coplus%20f%28R%2CK%29)

     ![TD_{i} (L||R) = R||L \oplus f(R,K)](https://latex.codecogs.com/gif.latex?TD_%7Bi%7D%20%28L%7C%7CR%29%20%3D%20R%7C%7CL%20%5Coplus%20f%28R%2CK%29)

解题：

$\\T_{16}(L_{15}||R_{15}) = L_{16} || R_{16} \\T_{17}(L_{16}||R_{16}) = R_{16} || L_{16} \\IP(IP^{-1}()) = None \\TD_1(R_{16} || L_{16} ) = L_{16}||R_{16}\oplus f(L_{16},K) \\ ~~~~~~~~~~~~~~~~~~~~ =R_{15}||L_{15} \oplus f(R_{15},K) \oplus f(L_{15},K) \\ ~~~~~~~~~~~~~~~~~~~~ =R_{15}||L_{15}$

$TD_1(L_{16}||R_{16}) =R_{16}||L_{16}\oplus f(R_{16},K) \\ ~~~~~~~~~~~~~~~~~~~~~~~~ =L_{15} \oplus f(R_{15},K) ||R_{15} \oplus f(R_{16},K)$

不成立

似乎都是每一列八个数字都是相近的8个呢，不知道啥用。

第一次0，后续逆序即可：

$\\A^{'} = A \oplus 111...1~~~~(Let~m = 111...1) \\Then ~~A^{'}\oplus B^{'} = A \oplus m \oplus B \oplus m = A \oplus B \\ ~~~~~~~~~~A \oplus B^{'}= (A \oplus B) \oplus m = (A \oplus B)^{'}$

可以分析得到，两方取反后异或等于两者直接异或，一方取反后异或，等于两方异或后取反

回顾加密过程（红色为未取反，黑色为取反后）

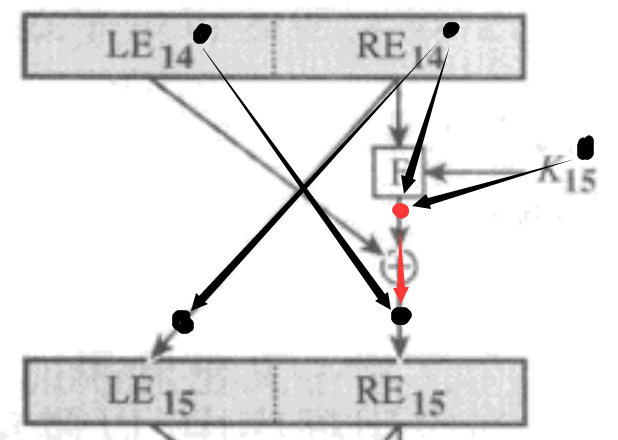
可见，取反后密文加密过程中，取反性质是传递的。故密文也会取反。

在明文选择攻击情况下，对于选择的明文M，攻击方可以获得的是C1 = E[K,M]和C2 = E[K,M'] 。这个时候我们知道（C2）' = E[K',M]. 我们只要去尝试不同的密钥T，如果加密后结果为C1,那么T就有可能是密钥，如果加密后结果为C2 ' 那么T'就有可能是密钥，复杂度由2^56变成2^55。

标签：网络安全

本文转载自: https://blog.csdn.net/weixin_44227244/article/details/126814896
版权归原作者 pianqiany 所有，如有侵权，请联系我们删除。