**LeetCode56.**合并区间
**难度:**中等
博主空间与往期力扣
**题目链接 **
作者原始思路
面向过程式的算法
class Solution {
public int[][] merge(int[][] intervals) {
var links = new ArrayList<Integer>();
for (int i = 0,des = 0;i < intervals.length;i++,des+=2) {
for (int j = 0; j < 2; j++) {
links.add(intervals[i][j]);
}
}
Collections.sort(links);
for (int i = 0; i + 1< links.size(); i++) {
if (links.get(i) == links.get(i+1)){
links.set(i+1,-1);
}
}
for (int i = 0; i < links.size(); i++) {
if (links.get(i) < 0) {
links.remove(i);
}
}
var isRead = new int[links.size()];
for (int[] interval : intervals) {
var left = links.indexOf(interval[0]);
var right = links.indexOf(interval[1]);
while (left <= right) {
isRead[left++]++;
}
}
var flag = false;
for (int j : isRead) {
if (j != 1) {
flag = true;
break;
}
}
if (flag) {
var res = new int[intervals.length][2];
var pre = 0;
var cur = 0;
var index = 0;
var count = 0;
for (int i = 0; i < links.size(); i++) {
pre = links.get(i++);
while (i + 1 < links.size() && isRead[i] >= 2) {
i++;
}
cur = links.get(i);
res[index][0] = pre;
res[index++][1] = cur;
count++;
}
var finalRes = new int[count][2];
for (int i = 0; i < count; i++) {
System.arraycopy(res[i], 0, finalRes[i], 0, 2);
}
return finalRes;
}else {
return intervals;
}
}
}
思想与代码简述
- 对于本题的思想,我采用的是计数的思想,即我们可以通过比较数字出现的个数,来判断哪些地方是重复出现的区域,哪些地方不是重复出现的区域,根据这个,我们就可以得出对应的没有重复区域的区间 - 1.总体的代码是先将二维数组里面的元素放入集合中,并对元素进行去重- 2.建立对应的计数数组,来判断每一个数字出现的个数- 3.根据计数数组来输出区间
问题
反省
- 对于用纯面向过程的思想去解答这一道题,明显是不现实的,利用面向过程思维去解决,不仅代码量大,而且对于多种特殊情况还要另加讨论,博主的水平做不到呀
- 所以,我们要以面向对象的思维去思考这一道题,如果采用面向对象的思维去解决,得会就会发现代码量大大减少
- 因此,我得出了初步的结论,如果发现元素绑定性极强的题目,我们就要考虑对象对象的算法思想
官方解法-区间排序算法
题目解读
- 题目中要求得出若干区间中,合并重叠的区间,最终得出来一个完全不重叠的区间集合,因此,我们发现这个题目的解决是以区间展开的,区间里面有两个元素.即元素绑定性强,我们采取面向对象的思想去解决该问题
算法思想
- 我们可以首先将区间进行**排序,即以区间的左端进行排序,得到一个序列**
- **根据序列,**依次将序列中的每一个区间对象依次放入集合中
- 如果****发现区间有重叠,就进行修改
案例分析
- intervals = [[1,3],[2,6],[8,10],[15,18]] - **排序后得出 [[1,3],[2,6],[8,10],[15,18]] **- 依次放入集合即 [1,3] -> [2,6] 此刻发现,[2,6]与[1,3]有重叠部分,所以将第一次的[1,3]改为[1,6]- ...
代码实现
class Solution {
public int[][] merge(int[][] intervals) {
if (intervals.length == 0) {
return new int[0][2];
}
Arrays.sort(intervals,(o1,o2) -> o1 [0] - o2[0]);
var merge = new ArrayList<int[]>();
for (int[] interval : intervals) {
var left = interval[0];
var right = interval[1];
if (merge.size() == 0 || merge.get(merge.size() - 1)[1] < left) {
merge.add(new int[]{left,right});
} else {
merge.get(merge.size() - 1)[1] = Math.max(merge.get(merge.size() - 1)[1], right);
}
}
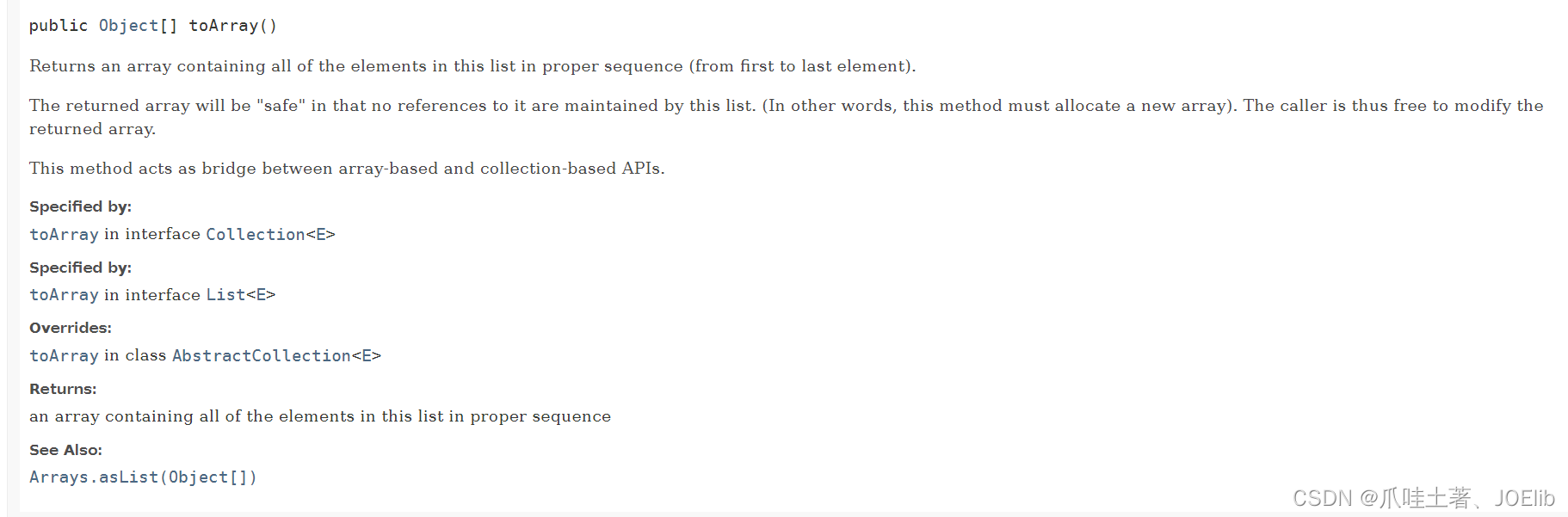
return merge.toArray(new int[merge.size()][]);
}
}
代码分析
- 1.先校验传进来的二维数组是长度为0,如果是则直接返回(可不写,题目中没有这个范围)
- 2.Arrays.sort(intervals,(o1,o2) -> o1 [0] - o2[0]) -
- 2.1调用的是这个sort方法,由API可知,我们传参一个int[][]的类型是符合泛型机制的(我们没有指定泛型,所以以运行时类型判断即Object判断,int[][]是Object的子类,可以传参)- 2.2由API可知,第二个参数是Comparetor接口及其子类- 2.2.1在这里,由于Comparetor接口是函数式接口,所以我们可以利用Lambda表达式或方法引用,这里,我采用了可读性更高而且更容易书写的Lambda表达式,以表示升序- 2.2.2(o1,o2) -> o1[0] - o2[0]的效果就是按照每一个区间左端数字的大小对区间对象进行升序排序- 2.3为什么要排序- 2.3.1如果没有排序,当示例是[2,3][1,2],按照算法思想,不可以直观的看出来哪里是重复了,所以要排序,如果还不明白,看下去 - 3.建立一个集合,专门用于存放结果,泛型指定为int[],即每一个元素都是一个区间对象
- 4.遍历二维数组 - 4.1left=>区间左端,即第一个元素- 4.2right=>区间右端,即第二个元素- 4.3如果merge集合里面没有一个元素,说明放入的区间不可能有人与他重复,直接放入- 如果merge集合中的最后一个区间的右端点比新区间的左端点都要小,说明新加入的区间不可能与前面的区间重复,直接加入- 注意:这里也可以放入interval- 4.4否则,说明了区间一定有重复的部分,此刻,由于我们用左端点对区间进行排序,所以,前面区间的左端点一定小于等于后面的,即一定在最左边,不可能有更左边的情况,所以不需要修改- 4.5我们主要讨论右端点的修改,即原有右端点和新增右端点,在两者中取较大值即可
- 5.最后,调用toArray()方法,返回对应的数组 - 注意:由于Java语法,里面需写成int[merge.size()][]-
结论
当我们遇到这种元素绑定性极强的题目时,我们不要拆开去写,我们要把他们看作是一个整体,以整体出发,寻求最优的算法,最后总结必须要掌握的几点
** 1.算法思想如何****** 2.如何调用API***
*** 3.什么时候使用该思维方式***
本文转载自: https://blog.csdn.net/JOElib/article/details/124514158
版权归原作者 爪哇土著、JOElib 所有， 如有侵权，请联系我们删除。
版权归原作者 爪哇土著、JOElib 所有， 如有侵权，请联系我们删除。