【维吉尼亚密码编写】
1. Equipment
(1) operating system version :WIN 10
(2) CPU instruction set: x 64
(3) software :Visual Studio 2019
2. process
Problem background analysis
Playfair密码编写(或者采用维吉尼亚密码编写,输入明文长度是任意的)
明文:量子通信保密技术的诞生和快速发展主要取决于以下两个因素: a、经典保密通信面临着三个难以彻底解决的关键问题,即密钥协商、身份识别和窃听检测,这些问题的有效解决需要新技术。b、在对新技术的探索中,人们发现了量子内在的安全特性及其可能的应用。
请写出你的密码机输出结果。
可以采用Playfair密码或者Vigenère密码,这里我采用的是Vigenère cipher完成信息加密。
在Vigenere密码中,用户钥是一个有限序列,我们可以通过周期性(周期为d)将k扩展为无限序列,其中Ki=K(i mod d),从而得到工作钥。如果用Φ和θ分别表示密文和明文字母,则Vigenere密码的变换公式为:Φ≡(θ+ki)(mod n)该密码体制有一个参数n。
在加解密时,同样把英文字母映射为0~25的数字再进行运算,并按一组进行变换。明文空间、密文空间及密钥空间都是长度为n的英文字母串的集合。对应的密码表如下:

Solution
根据上述的原理,采用C++实现如下:
code:
#include <iostream>
#include <string>
#include <string.h>
#pragma warning(disable:4996)
/*
* @Author:timerring
* @Date: 2021-10-20 14:05:49
* @LastEditTime: 2021-10-22 08:11:15
* @FilePath:c:\Users\timerring\Vigenere.cpp
*/
using namespace std;
const int N = 26;
//定义二维密码表
char v[N][N] = { {'A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z'} };
int number(char x)
{//把行号字母对应到数字空间上
char y = 'a';
for (int i = 0; i < N; i++)
{
if (x == (y + i)) return i;
}
}
void encryption(string msg, string key)
{//定义加密过程
cout << "plaintext:";
cin >> msg;
cout << "key:";
cin >> key;
int mlen, klen;
//获取明文和密钥的长度
mlen = msg.length();
klen = key.length();
char* p, * q, * t;//明文,初始密钥,密钥串
//把string换成char
p = new char[msg.length() + 1];
//用strcpy函数进行对应的复制
strcpy(p, msg.c_str());
q = new char[key.length() + 1];
strcpy(q, key.c_str());
t = new char[msg.length() + 1];
int j = 0;
for (int i = 0; i < mlen; i++)
{
t[i] = q[j];
j++;
j = j % klen;
}
cout << "ciphertext:";
for (int i = 0; i < mlen; i++)
//按位输出密文字符
cout << v[number(t[i])][number(p[i])];
cout << endl;
}
void decryption(string c, string key)
{//定义解密过程
cout << "ciphertext:";
cin >> c;
cout << "key:";
cin >> key;
int clen, klen;
clen = c.length();
klen = key.length();
char* p, * q, * t;//密文,初始密钥,密钥串
//将string换成char
p = new char[c.length() + 1];
//用strcpy函数进行对应的复制
strcpy(p, c.c_str());
q = new char[key.length() + 1];
strcpy(q, key.c_str());
t = new char[c.length() + 1];
int j = 0;
for (int i = 0; i < clen; i++)
{
t[i] = q[j];
j++;
j = j % klen;
}//生成密钥
cout << "plaintext:";
for (int i = 0; i < clen; i++)
for (int j = 0; j < N; j++)
if (v[number(t[i])][j] == p[i]) { cout << char(j + 97); break; }
cout << endl;
}
int main()
{
for (int i = 1; i < N; i++)
{
for (int j = 0; j < N; j++)
{
v[i][j] = v[i - 1][(j + 1) % N];
}//将方阵进行初始化
}
cout << "You are welcome to use Vigenere in SDU\n" << endl;
cout << "Please enter the corresponding operation number:" << endl;
int flag;
do {
cout << "1.Encrypt\n2.Decrypt\n";
cin >> flag;
string m, key;
if (flag == 1)encryption(m, key);
else if (flag == 2) decryption(m, key);
else
break;
} while (flag != 3);
return 0;
}
Test sample:
由Vigenere密码的基本原理可知,它未能完成中文密码的编写,因此我们采用将明文翻译为英语,再对其进行加密,样例中取密钥为sduqingdao,密码机的输出如下:
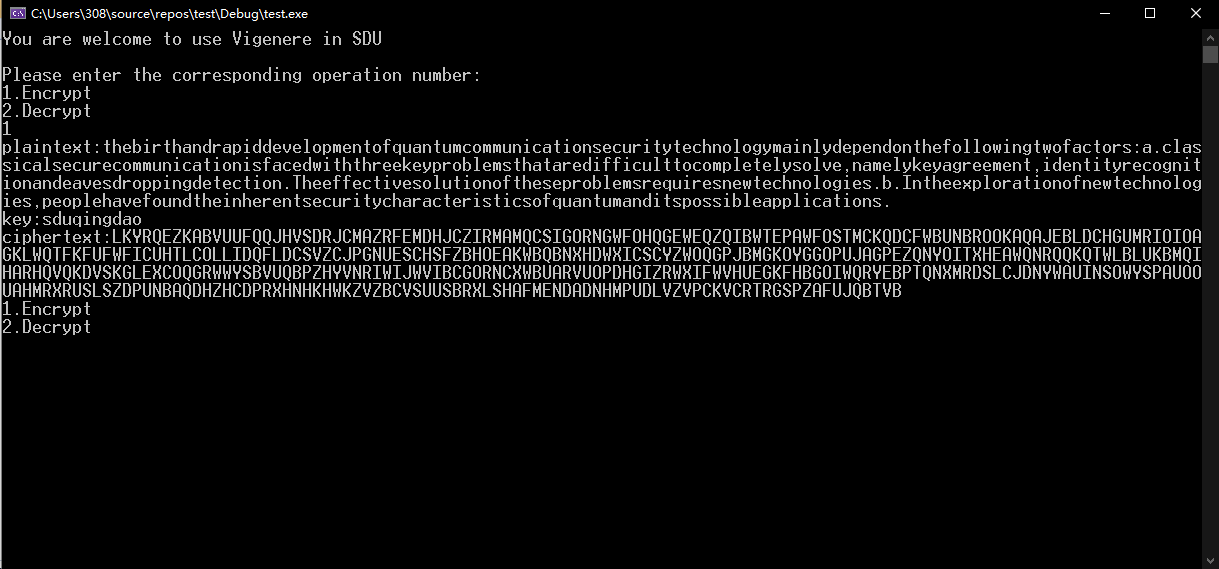
3. summary and harvest
我对于Vigenère密码的理解加深了,Vigenère密码通过使用多个字母代换表,达到同一个字母在不同位置会被替换成不同密文的效果,方法是用一个密钥选择使用哪个字母代换表,依次使用多个字母表,当密钥的字母使用结束的时候再从头排列。
这样的密码比单表代换安全系数略高,可以通过加长密钥的方式确保相对的安全性。通过简单的密码分析破译的难度略大,但是如果密文足够长,其间会有大量重复的密文序列出现。通过计算重复密文序列间距的公因子,分析者可能猜出密钥词的长度。同时通过查阅文献找到了它的破译方法 [1] ,可以使用卡西斯基试验和弗里德曼试验来得到密钥的长度,一旦能够确定密钥的长度,密文就能重新写成多列,列数与密钥长度对应。这样每一列就是一个凯撒密码,而此密码的密钥则对应于Vigenère密码密钥的相应字母。使用与破译凯撒密码类似的方法,就能将密文破译。
同时我也遇到了一些困难,在使用strcpy函数进行字符复制的时候,编译器报错, ‘strcpy’: This function or variable may be unsafe. Consider using strcpy_s instead. To disable deprecation, use _CRT_SECURE_NO_WARNINGS. See online help for details,通过查询,得知是因为strcpy的安全性不高,可以采用两种方法解决:1.使用strcpy_s函数 2.使用#pragma预处理命令禁止警告
4.Reference
[1]杨振,杨帆,夏山,高钏淏,万贺.一种基于卡西斯基试验的密钥破译算法分析[J].网络安全技术与应用,2020(10):52-55.
初学信息安全,可能存在错误之处,还请各位不吝赐教。
受于文本原因,本文相关算法实现工程无法展示出来,现已将资源上传,可自行点击下方链接下载。
维吉尼亚密码原理详解及算法实现工程文件
版权归原作者 timerring 所有, 如有侵权,请联系我们删除。