你可能听说过核密度估计(KDE：kernel density estimation)或非参数回归（non-parametric regression）。你甚至可能在不知不觉的情况下使用它。比如在Python中使用seaborn或plotly时，distplot就是这样，在默认情况下都会使用核密度估计器。但是这些大概是什么意思呢?

也许你处理了一个回归问题，却发现线性回归不能很好地工作，因为特性和标签之间的依赖似乎是非线性的。在这里，核回归（kernel regression）可能是一种解决方案。

在这篇文章中，我们通过示例，并试图对内核估计背后的理论有一个直观的理解。此外，我们还看到了这些概念在Python中的实现。

核回归

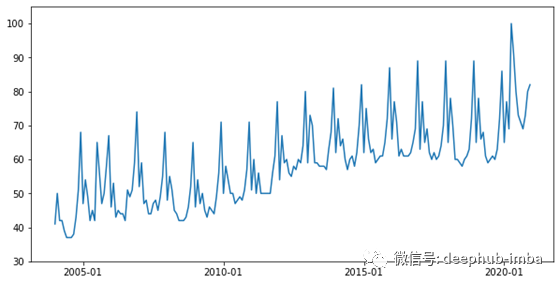
图1:全球谷歌搜索“chocolate”;x轴:时间，y轴:搜索百分比

让我们从一个例子开始。假设你是一个数据科学家，在一家糖果工厂的巧克力部门工作。

你可能想要预测巧克力的需求基于它的历史需求，作为第一步，想要分析趋势。2004-2020年的巧克力需求可能类似于图1中的数据。

显然，这是有季节性的，冬天的需求会增加，但是由于你对趋势感兴趣，你决定摆脱这些波动。为此，你可以计算窗口为b个月的移动平均线，也就是说，对于每一个时刻t，你计算从t-b到t+b的时间段内需求的平均值。

更正式地说，如果我们有一段时间内观察到的数据X(1)，…，X(n)，即一个时间序列，窗口为b的移动平均值可以定义为

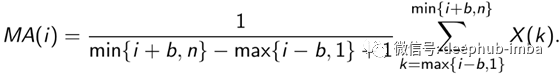
从下图（图2）中可以看出，移动平均值是原始数据的平滑版本，平滑程度取决于带宽。带宽越大，函数越平滑。

图2:窗口带宽为6、24和42的移动平均;x轴:时间，y轴:搜索百分比

带宽的选择至关重要，但不清楚如何选择带宽。如果带宽太小，我们可能无法摆脱季节性波动。如果带宽太大，我们可能无法捕捉到趋势。例如，如果我们选择带宽b = 0，则具有原始数据及其季节性。相反，如果b = n，我们仅获得所有观测值的平均值，而看不到任何趋势。

在此示例中，b = 6个月是“平滑”季节性因素的合理选择，因为我们计算的是整个年度（13个月）的平均值。但是，b = 12或b = 18是同等有效的选择。根据b的选择，我们将更多的权重赋予与时刻t（b = 12）相同的季节或相反季节（b = 6或b = 18）的观测值。减轻此问题的可能解决方案是为观察值赋予不同的权重，从而计算加权平均值而不是简单平均值。

理论上讲，接近时间t的观测比更远的观测更重要，并且权重更大。这使我们可以选择更大的带宽b，同时将更多的权重分配给更重要的观察。例如，对于时间t的观测，我们可以赋予权重1；对于距离i为i = 1，…，11的观测，我们可以赋予1-i / 12权重；对于i = 1，...， b-1和带宽b（请参见图3）。

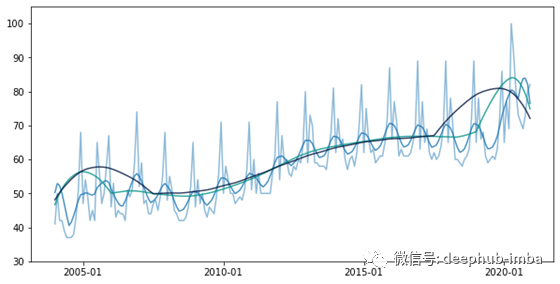
图3：带宽为6、24和42的加权移动平均线；x轴：时间，y轴：搜索百分比

这是核估计背后的基本思想：对不同距离的观测值赋予不同的权重。

权重(1-i/b) 的上述选择相当随意，其他权重也可以理解。我们可以将加权移动平均值归纳如下：令b为带宽，K为核，即具有某些其他性质的函数，例如非负[K（x）≥0]对称性[K（x）= K （-x）]和归一化[K上的积分为1]。许多内核都支持间隔[-1，1]，这意味着它们在间隔之外为0。

内核的重要示例是| x |的Epanechnikov 内核K(x) = 3/4 (1-x²) 当 |x| ≤ 1 和高斯核K（x）= 1 / sqrt（2π）exp（-x²/ 2）。

基于内核K和带宽b，我们将NWE（Nadaraya-Watson Estimator）定义为：

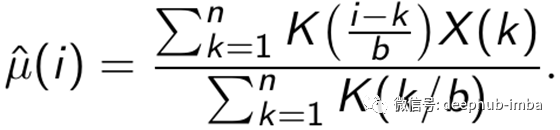
在图4中，我们看到具有高斯核且带宽b = 12的NWE。内核和带宽的选择仍然很重要，但是具有频繁使用内核的估计器（例如Epanechnikov，Quartic或Gaussian）在带宽选择方面比移动平均估计器更健壮。

注意，简单移动平均估计量本身是具有统一核K（x）= 1/2的核估计量。加权移动平均估计器也是一个内核估计器，wiki里面有一个和函数的整理列表，有兴趣的可以仔细查看https://en.wikipedia.org/wiki/Kernel_(statistics)#Kernel_functions_in_common_use

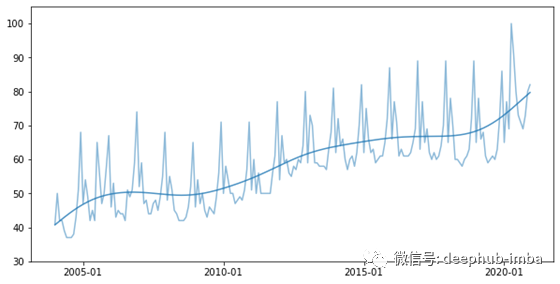
图4：具有高斯核和带宽12的NEW；x轴：时间，y轴：百分比搜索

进一步说明：首先，通常基于重新定标的时间（即i / n而不是i）来定义NEW，并且公式也会相应变化。其次，对于距离变化的观测，可以更普遍地定义估算器。

核密度估计

让我们考虑另一个例子。由于某种原因，你可能会对德国的汽油价格感兴趣。因此，你可以上网搜索所有14,000个加油站的当前价格。图5中是该数据的常见表示形式：直方图。直方图显示汽油价格的分布。块的带宽是关键参数，不同的选择会导致不同的直方图（类似于移动平均估计器的不同带宽）。

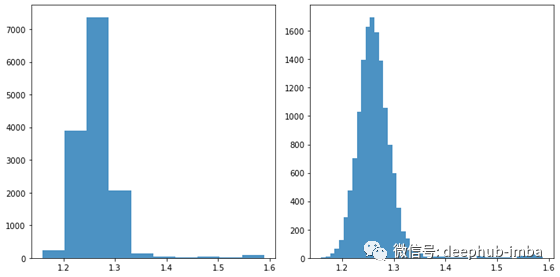
图5：直方图显示德国（05/12/2020）分别有10个和50个垃圾箱的天然气价格频率；x轴：以EUR为单位的汽油价格；y轴：频率；

如果我们假设天然气价格的分布是连续的，我们可能更喜欢估计和可视化基础分布的密度函数。这个想法的原理很简单：对于天然气价格范围内的任何一点，我们都会计算价格接近该点的频率，并给予较接近的价格更多的权重，而向较远的价格赋予较小的权重。

如果“距离决定权重”是确定正确的， 那么我们将重点关注这个调节，这就是是内核回归背后的想法。

数据X（1），…，X（n）的核密度估计器的定义与NWE非常相似。给定一个内核K且带宽h> 0，定义

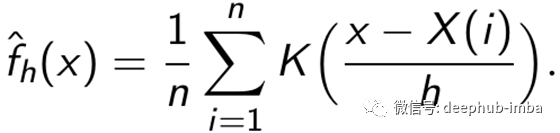
通常使用与核回归情况相同的核函数（例如，高斯，Epanechnikov或Quartic）。核密度估计可以解释为提供关于底层数据生成过程的分布的平滑的直方图。内核和带宽的选择同样至关重要（有关不同的估算器，请参见图6）。

图6:不同内核(上:Epanechnikov，下:高斯)和不同带宽(左:0.05，右:0.1)下天然气价格密度的KDE;x轴:天然气价格(欧元);轴:频率

在Python中实现

为了展示内核回归，我们使用Google搜索一词中的Chocolate一词的数量，该词可在Google Trends中下载。如果保存为kde_chocolate.csv，则以下Python脚本将计算NWE并绘制图4：

 import numpy as np
 import pandas as pd
 import matplotlib.pyplot as plt
 from statsmodels.nonparametric.kernel_regression import KernelReg
 
 df = pd.read_csv('kde_chocolate.csv')
 
 n = df.shape[0]
 kde = KernelReg(endog=df['chocolate'], exog=np.arange(n), var_type='c', bw=[12])
 
 estimator = kde.fit(np.arange(n))
 estimator = np.reshape(estimator[0],n)
 
 fig, ax = plt.subplots(figsize=(10,5))
 ax.plot(df['month'], df['chocolate'], '-',alpha=0.5)
 ax.plot(df['month'], estimator, '-', color='tab:blue', alpha=0.8)
 ax.set_ylim(bottom=30, top=105)
 ax.set_xticks(['2005-01','2010-01','2015-01','2020-01'])
 
 plt.show()

考虑到德国不同加油站的汽油价格，其中“ station_uuid”和“ e5”列保存在kde_gas_data.csv中，可通过以下脚本获得类似于图6的图。可以通过Azure Repo获取数据（https://dev.azure.com/tankerkoenig/_git/tankerkoenig-data）。

 import pandas as pd
 import matplotlib.pyplot as plt
 from sklearn.neighbors import KernelDensity
 import numpy as np
 
 # Load data and remove outliers
 df = pd.read_csv('kde_gas_data.csv')[['station_uuid', 'e5']]
 df = df.groupby(['station_uuid']).mean()
 df = df[df['e5'] > 0]
 df = df.sort_values('e5')[round(df.shape[0]*0.001):round(df.shape[0]*0.999)]
 
 # Calculate and plot KDEs
 fig, ax = plt.subplots(2, 2, sharex=True, sharey=True, figsize=(10,6))
 X = df['e5'][:,np.newaxis]
 X_plot = np.linspace(1,1.6,1000)[:,np.newaxis]
 zeros = np.zeros(1000)
 
 kde = KernelDensity(kernel='epanechnikov', bandwidth=0.05).fit(X)
 log_dens = kde.score_samples(X_plot)
 ax[0, 0].fill_between(X_plot[:, 0], zeros, np.exp(log_dens), fc='#AAAAFF')
 
 kde = KernelDensity(kernel='epanechnikov', bandwidth=0.1).fit(X)
 log_dens = kde.score_samples(X_plot)
 ax[0, 1].fill_between(X_plot[:, 0], zeros, np.exp(log_dens), fc='#AAAAFF')
 
 
 kde = KernelDensity(kernel='gaussian', bandwidth=0.05).fit(X)
 log_dens = kde.score_samples(X_plot)
 ax[1, 0].fill_between(X_plot[:, 0], zeros, np.exp(log_dens), fc='#AAAAFF')
 
 kde = KernelDensity(kernel='gaussian', bandwidth=0.1).fit(X)
 log_dens = kde.score_samples(X_plot)
 ax[1, 1].fill_between(X_plot[:, 0], zeros, np.exp(log_dens), fc='#AAAAFF')
 
 plt.show()

总结

在两种情况下（内核回归和内核密度估计），我们都必须选择内核和窗口的带宽。由于常用的内核具有相似的形状（请参见图7），因此带宽的选择更为关键。关于带宽选择，有大量文献。在应用程序中，两种方法占主导地位：拇指法则带宽估计器（例如Silverman的经验法则）和交叉验证（尤其是用于内核回归）。

图7：常用的内核函数：高斯（左上），Epanechnikov（右上），四次（左下），均匀（右下）

由于大多数内核函数是平滑的（或至少是连续可微的），因此得出的估计量也是平滑的。因此，呈现形式的核回归仅对于足够平滑的回归/密度函数才有意义。

NWE是一类更广泛的非参数估计器的特例，即局部多项式估计器。

基于内核的估计器非常有用，并适用于许多情况。甚至k最近邻算法也可以被视为具有统一内核和可变带宽的基于内核的估计器。正如我们可以采用其他内核一样，这种范例为我们提供了新的可能性，从而为不同的点赋予了不同的权重。

我相信基于核的估计的概念对数据科学家来说很重要，希望你能建立一些直观的理解。

作者：Florian Heinrichs

deephub翻译组

原文地址：https://towardsdatascience.com/kernel-density-estimation-and-non-parametric-regression-ecebebc75277