用于AB测试的减少方差方法总结和对比

点击上方“Deephub Imba”,关注公众号,好文章不错过 !

为什么我们需要方差减少?

当我们进行在线实验或A/B测试时，我们需要确保我们的测试具有很高的统计能力，这样如果我们的推断确实存在的话，我们就有很高的概率发现和验证它。影响统计能力的因素有哪些?样本大小、实验度量的抽样方差、显著性水平和效应大小。

提高能力的规范方法是增加样本量。然而，对于在线实验，我们使用的样本范围是有限的，因为MDE（最小预期提升幅度）与1/sqrt(sample_size)成正比。此外，在现实中获取更多的样本或进行更长时间的实验来增加样本量可能并不容易或并不可行。

我们能做的第二件事是减少实验指标的抽样方差。最简单的方法就是转换指标。Winsorize、二值化或其他更复杂的指标转换将有助于显著减少方差。然而，度量转换会引入偏差。所以这种方法存在偏差-方差权衡的问题。

还有许多传统的减少方差方法被开发和应用，并且以提高实验的灵敏度/能力。在本文中，我将介绍一些流行的方差减少方法，并演示一些Python中的简单示例:

1. Stratification 和 post-stratification
2. CUPED (controlled-experiment using pre-experiment data)
3. Variance-Weighted Estimators

还有一些基于ML的方法:

1. CUPAC(control using predictions as covariates)
2. MLRATE(machine learning regression-adjusted treatment effect estimator)

Stratification

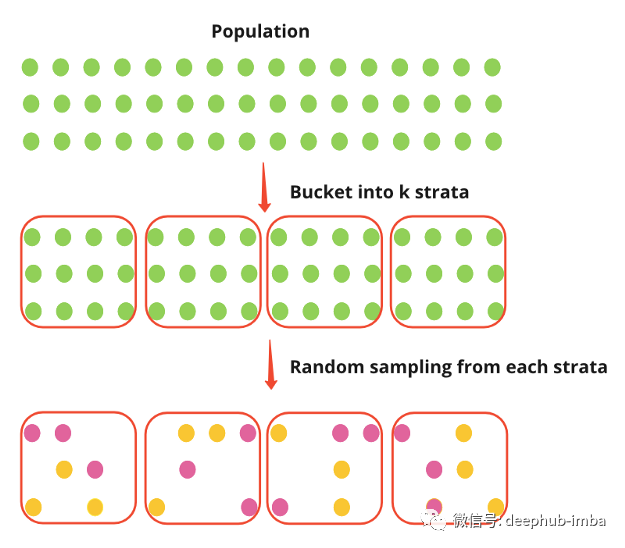
分层（Stratification）抽样将总体分为k个层次(如国家)，然后实验从每个层次独立随机抽样个体。设Y_strat为分层抽样下的实验效果，设p_k表示来自k层的样本容量所占的比例。由下式可知，实验效果为各层实验效果的综合平均值，这是无偏的。该方差是层内方差的加权平均值，有效地消除了层间方差。该方差小于简单随机抽样下的方差，其中包括层内方差和层间方差。

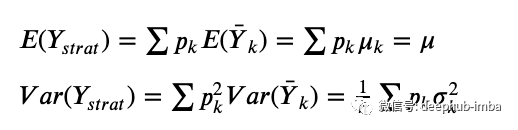
利弊

分层方法提供了对实验效果的无偏估计，并有效地消除了层间差异。然而，在实践中，通常很难在实验前实施分层抽样。

“在网络世界中，数据的收集是随到达时间相关的，所以我们通常无法从提前形成的层中进行采样。” （Deng, Xu, Kohavi, & Walker, 2013）

在实践中，实施分层抽样既复杂又昂贵。它“需要一个队列系统和多台机器的使用。” (Xie & Aurisset, 2016)

虽然以上两段总结了分层抽样的问题，但是因为技术的发展就目前看这些问题基本上不是问题，但是他们会使我们系统变得更复杂。

Post-stratification

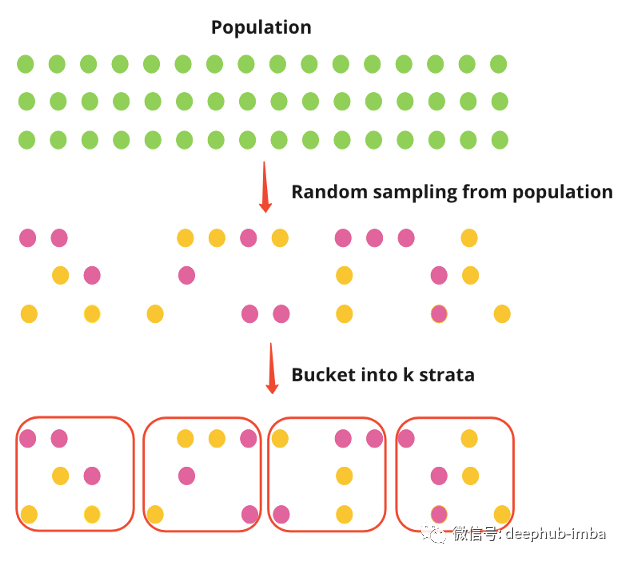
在实践中，后分层比分层更常见。分层后首先随机抽样总体，然后将抽样的个体放入层中。与分层相似，后分层也能达到类似的方差减少。

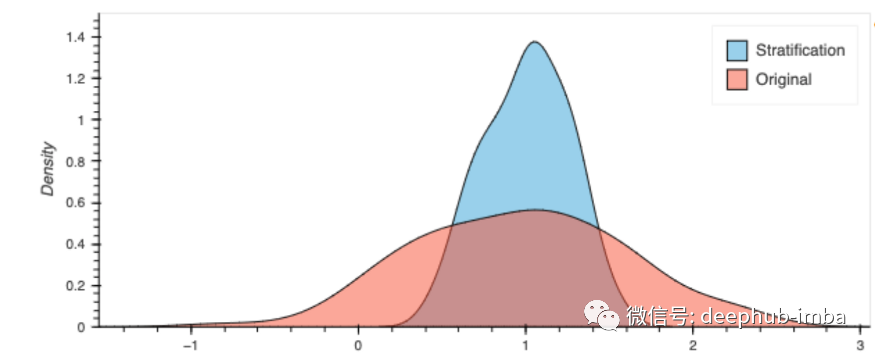
这里有一个非常简单的例子，我们从四个不同的正态分布(4层)中生成数据，随机将个体分配到实验组和对照组，在实验组中添加一个实验效果，并通过bootstrapping可视化实验效果。实验效果计算为未分层实验与对照实验之间的平均差值和各分层实验层的平均差值的平均值。

从我们简单的例子中，我们确实看到分层的方差减少。至关重要的是，平均值没有变化，所以方差已经减少，我们应该能够更好地看到任何实验对平均值的影响。

import pandas as pd
import numpy as np
import hvplot.pandas
from scipy.stats import pearsonr
from scipy.optimize import minimize

def generate_strata_data(treatment_effect, size):
    # for each strata, generate y from a normal distribution
    df1 = pd.DataFrame({'strata': 1, 'y': np.random.normal(loc=10, scale=1, size=size)})
    df2 = pd.DataFrame({'strata': 2, 'y': np.random.normal(loc=15, scale=2, size=size)})
    df3 = pd.DataFrame({'strata': 3, 'y': np.random.normal(loc=20, scale=3, size=size)})
    df4 = pd.DataFrame({'strata': 4, 'y': np.random.normal(loc=25, scale=4, size=size)})
    df = pd.concat([df1, df2, df3, df4])
    # random assign rows to two groups 0 and 1 
    df['group'] = np.random.randint(0,2, df.shape[0])
    # for treatment group add a treatment effect 
    df.loc[df["group"] == 1, 'y'] += treatment_effect
    return df   

def meandiff(df):
    return df[df.group==1].y.mean() - df[df.group==0].y.mean()

def strata_meandiff(df):
    get_sum = 0
    for i in df.strata.unique():
        get_sum += meandiff(df[df.strata==i])
    return get_sum/len(df.strata.unique())

meandiff_lst = []
strata_meandiff_lst = []
for i in range(100):
    df = generate_strata_data(treatment_effect=1, size=100)
    meandiff_lst.append(meandiff(df))
    strata_meandiff_lst.append(strata_meandiff(df))
    
(
    pd.DataFrame(strata_meandiff_lst).hvplot.kde(label='Stratification') 
    * pd.DataFrame(meandiff_lst).hvplot.kde(label='Original')
)

CUPED

CUPED(Controlled-experiment using pre-experiment data)是由来自微软的Alex Deng、Ya Xu、Ron Kohavi和Toby Walker于2013年首次提出的，目前已被广泛应用于Netflix、bookings、TripAdvisor等大型科技公司。CUPED使用预实验数据X(例如，预实验值Y)作为控制协变量:

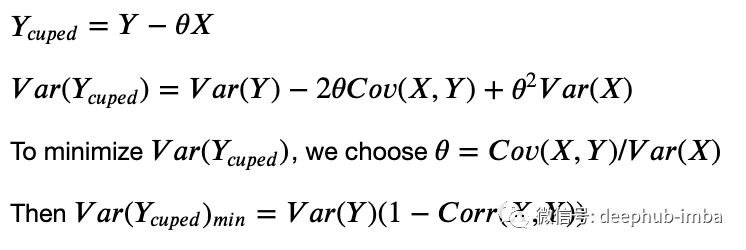
也就是说，Y的方差减少了(1-Corr(X, Y))。我们需要X和Y之间的相关性很高，才能使CUPED工作得很好。在原论文中，建议将Y的预实验值作为X。

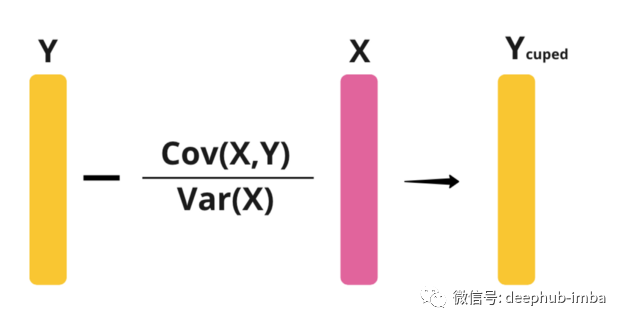
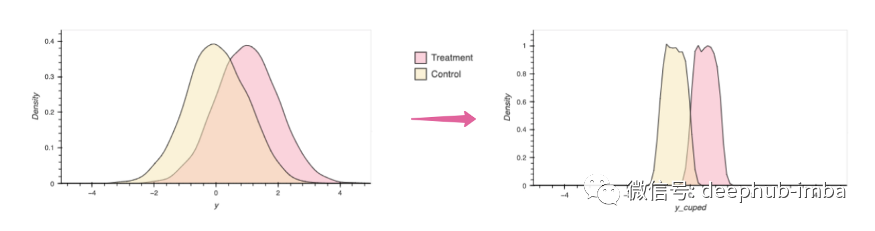
这里有一个样本的例子。我们可以看到，对照组和实验组的Y的方差都减小了，Y_cuped与Y的方差之比为0.2789，与根据上述理论方程得到的(1-Corr(X,Y))值相同。减少方差可以减少这两个分布之间的重叠，从而更容易看到实验效果。

def generate_data(treatment_effect, size):
    # generate y from a normal distribution
    df = pd.DataFrame({'y': np.random.normal(loc=0, scale=1, size=size)})
    # create a covariate that's corrected with y 
    df['x'] = minimize(
        lambda x: 
        abs(0.95 - pearsonr(df.y, x)[0]), 
        np.random.rand(len(df.y))).x
    # random assign rows to two groups 0 and 1 
    df['group'] = np.random.randint(0,2, df.shape[0])
    # for treatment group add a treatment effect 
    df.loc[df["group"] == 1, 'y'] += treatment_effect
    return df    

df = generate_data(treatment_effect=1, size=10000)
theta = df.cov()['x']['y'] / df.cov()['x']['x']
df['y_cuped'] = df.y - theta * df.x

(
    df.hvplot.kde('y', by='group', xlim = [-5,5], color=['#F9a4ba', '#f8e5ad']) 
    + df.hvplot.kde('y_cuped', by='group', xlim = [-5,5], color=['#F9a4ba', '#f8e5ad'])
)

这里我们多次模拟我们的实验，计算对照组和实验组的平均差值，得到的效果分布。注意Y_cuped不是y的无偏估计量，但是Y_cuped的均值差是y的均值差的无偏估计量。根据下图，很明显，在我们的简单情况下，CUPED降低了我们实验的方差。

def generate_data(treatment_effect, size):
    # generate y from a normal distribution
    df = pd.DataFrame({'y': np.random.normal(loc=0, scale=1, size=size)})
    # create a covariate that's corrected with y 
    df['x'] = minimize(
        lambda x: 
        abs(0.95 - pearsonr(df.y, x)[0]), 
        np.random.rand(len(df.y))).x
    # random assign rows to two groups 0 and 1 
    df['group'] = np.random.randint(0,2, df.shape[0])
    # for treatment group add a treatment effect 
    df.loc[df["group"] == 1, 'y'] += treatment_effect
    return df   

def meandiff(df):
    return df[df.group==1].y.mean() - df[df.group==0].y.mean()

def cuped_meandiff(df):
    theta = df.cov()['x']['y'] / df.cov()['x']['x']
    df['y_cuped'] = df.y - theta * df.x
    return df[df.group==1].y_cuped.mean() - df[df.group==0].y_cuped.mean()

meandiff_lst = []
cuped_meandiff_lst = []
for i in range(200):
    df = generate_data(treatment_effect=1, size=100)
    meandiff_lst.append(meandiff(df))
    cuped_meandiff_lst.append(cuped_meandiff(df))
    
pd.DataFrame(cuped_meandiff_lst).hvplot.kde(label='CUPED') * pd.DataFrame(meandiff_lst).hvplot.kde(label='Original')

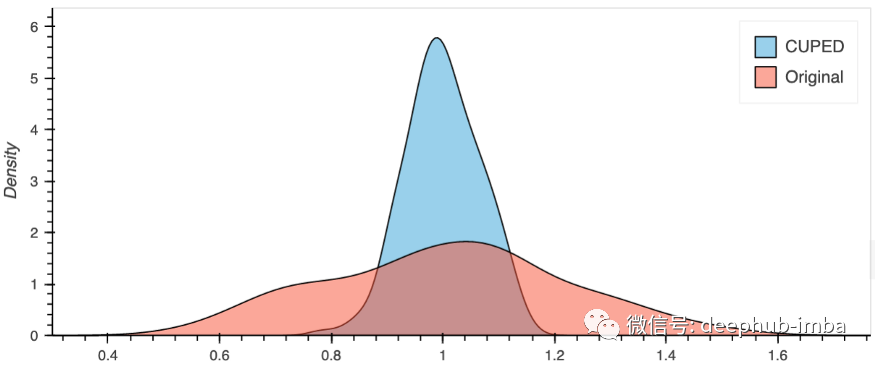
利弊

CUPED超级容易使用和实现。然而协变量的选择可能是比较复杂的，特别是当目标变量的预实验测量是不可用的。协变量必须与目标测量相关，但与实验无关。此外，原始论文没有说明有多个协变量的场景。这篇博文讲述了将CUPED从一个协变量扩展到多个协变量的代数过程。另一个解决方案是使用ML构造控制变量，我们将在后面讨论。

Variance-Weighted Estimators

Variance-Weighted Estimators（方差加权估计法）是由来自Facebook和Lyft的Kevin Liou和Sean Taylor在2020年开发的。该方法的主要思想是给具有较低的实验前方差的用户更多的权重。

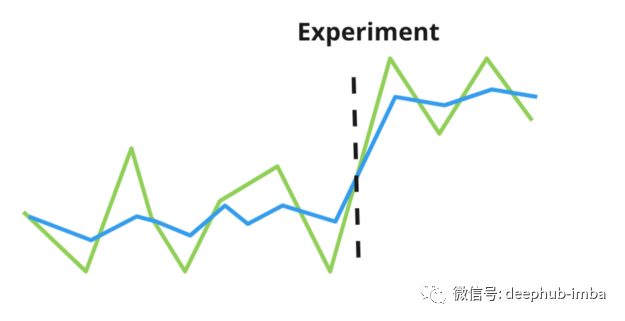
这种方法放宽了同方差的假设，而是假设每个个体都可以有自己的度量方差。例如，上图显示了两个个体，其中一个(绿线)的方差高于另一个(蓝线)。

下式中，为了最小化实验效果的方差，我们用方差的倒数来加权每个用户。

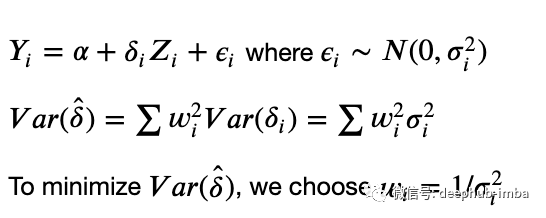
与CUPED类似，方差加权估计也使用预实验数据。论文中提出了几种估计方差的方法，包括使用实验前时间序列数据的经验方差，建立ML模型，使用经验贝叶斯估计。最简单的方法是用经验方差。

加权会引起偏差，所以为减少偏差提出了基于桶用户的预实验方差的实验方法，计算每个桶内实验效果的均值和经验方差，然后计算跨层加权实验效果。

因此，在实际应用中，我们将估计方差，将方差分成k层，用逆方差对各层进行加权，计算加权实验效果。

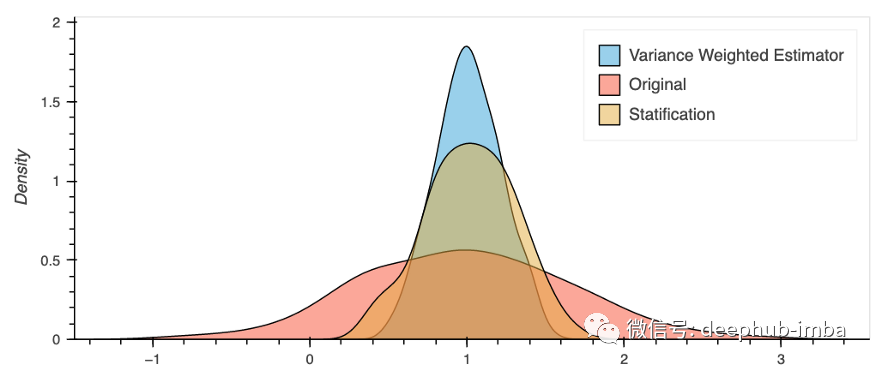
这里有一个非常简单的例子来演示这种方法。我从四个层次开始我们知道每个层次的度量方差。然后用各层的逆方差来衡量实验效果。对于这个例子，除了分层方法外，方差加权估计还提供了方差减少的额外好处。

def generate_strata_data(treatment_effect, size):
    # for each strata, generate y from a normal distribution
    df1 = pd.DataFrame({'strata': 1, 'pre_experient_variance':1, 'y': np.random.normal(loc=10, scale=1, size=size)})
    df2 = pd.DataFrame({'strata': 2, 'pre_experient_variance':2, 'y': np.random.normal(loc=15, scale=2, size=size)})
    df3 = pd.DataFrame({'strata': 3, 'pre_experient_variance':3, 'y': np.random.normal(loc=20, scale=3, size=size)})
    df4 = pd.DataFrame({'strata': 4, 'pre_experient_variance':4, 'y': np.random.normal(loc=25, scale=4, size=size)})
    df = pd.concat([df1, df2, df3, df4])
    # random assign rows to two groups 0 and 1 
    df['group'] = np.random.randint(0,2, df.shape[0])
    # for treatment group add a treatment effect 
    df.loc[df["group"] == 1, 'y'] += treatment_effect
    return df   

def variance_weighted_meandiff(df):
    weighted_effect_sum = 0
    weights_sum = 0
    for i in df.strata.unique():
        #For each strata, we then calculate its average treatment effect
        treatment_effect_strata = meandiff(df[df.strata==i])
        # estimate its weight based on the inverse within-group estimated variance (such as mean)
        weights_strata = 1/df[df.strata==i]['pre_experient_variance'].mean()
        # calculate the sum of weighted treatment effect
        weighted_effect_sum +=  treatment_effect_strata *  weights_strata
        # calculate the sum of weights
        weights_sum += weights_strata    
    return weighted_effect_sum/weights_sum

def strata_meandiff(df):
    get_sum = 0
    for i in df.strata.unique():
        get_sum += meandiff(df[df.strata==i])
    return get_sum/len(df.strata.unique())

meandiff_lst = []
variance_weighted_meandiff_lst = []
strata_meandiff_lst = []
for i in range(200):
    df = generate_strata_data(treatment_effect=1, size=100)
    meandiff_lst.append(meandiff(df))
    variance_weighted_meandiff_lst.append(variance_weighted_meandiff(df))
    strata_meandiff_lst.append(strata_meandiff(df))
   
(
    pd.DataFrame(variance_weighted_meandiff_lst).hvplot.kde(label='Variance Weighted Estimator')
    * pd.DataFrame(meandiff_lst).hvplot.kde(label='Original')
    * pd.DataFrame(strata_meandiff_lst).hvplot.kde(label='Statification')
)

利弊

方差加权估计将个体实验前的方差建模为权重，它可以用作其他方法（如 CUPED）的很好的扩展。当用户之间存在高度偏斜的方差并且预处理方差是处理后方差的良好指标时，它运行良好。

但是，当处理前方差的方差较低或实验前后的方差不一致时，方差加权估计量可能不起作用。此外，方差加权估计量不是无偏的。

基于机器学习的方法

近年来开发了几种基于 ML 的方差减少方法。我将简要介绍两种基于机器学习的方法——CUPAC 和 MLRATE。由于原始论文没有描述确切的算法和他们 ML 模型的细节，我只会谈谈我对高级思想的理解，而不是展示这些方法的例子。

CUPAC

CUPAC（Control Using Predictions As Covariates）由Doordash的Jeff Li、Yixin Tang和Jared Bauman于2020年引入，是CUPED的扩展。CUPAC 没有选择与对照无关的实验前协变量 X，而是使用机器学习模型的结果作为其控制变量。机器学习模型的目标是“最大化预测协变量（CUPAC）和目标度量之间的部分相关性”。

假设我们有实验前指标 X1、X2、X3 和 X4。本质上，该方法的作用是使用某种机器学习模型，使用 X1、X2、X3 和 X4 来预测 Y。然后，我们可以使用预测值作为 CUPED 中的控制协变量。

MLRATE

MLRATE（machine learning regression-adjusted treatment effect estimator）由Guo等人于2021年由Princeton 和Facebook提出。

与 CUPAC 类似，MLRATE 也使用 ML 模型从 X 预测 Y。我们将预测值称为 g(X)。MLRATE 不是从 Y 中减去 g(X)，而是将 g(X) 与实验指标一起包含在回归模型中，然后计算回归调整后的实验效果。下图展示了这个回归模型：

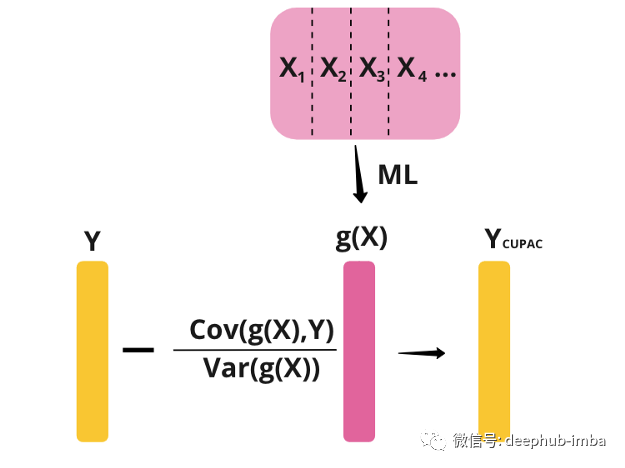
首先，我们从协变量向量或协变量矩阵 X 开始。然后我们学习并应用交叉拟合监督学习算法。交叉拟合用于避免过度拟合偏差。交叉拟合过程如下：我们将数据分成 k 个分割。对于每个分割，我们在当前分割中的样本上训练我们的数据并得到一个函数 g。然后我们使用当前分割中的X，得到当前分割的g(X)的预测值。

接下来，我们进行一个回归模型，其中我们使用以下回归量预测实验指标 Y：T — 实验指标，g(X) — 交叉拟合 ML 的预测值，以及 T(g(x)-g)。

α1 的 OLS 估计量是我们感兴趣的治疗效果。

其他基于机器学习的方法

业界还使用了其他基于机器学习的方法。例如，Yandex 的 Poyarkov 等人在 2016 年开发了 Boosted decision tree regression adjustment。

总体而言，本文总结了行业中一些流行的方差减少方法——post-stratification, CUPED, Variance-Weighted Estimators, 和基于机器学习的方法CUPAC and MLRATE。在实践中，CUPED 在科技公司中被广泛使用和生产化，基于 ML 的方法通常用于合并多个协变量。我们可以 结合多种方法来实现最佳方差减少也很常见。希望这篇文章对您有所帮助。谢谢！

致谢：非常感谢 Anthony Fu 和 Jim Bednar 为本文提供指导和反馈。感谢 Kevin Liou 和 Sean Taylor 澄清了我关于方差加权估计量的问题。

作者：Sophia Yang

引用

• https://exp-platform.com/Documents/2013-02-CUPED-ImprovingSensitivityOfControlledExperiments.pdfhttps://www.kdd.org/kdd2016/papers/files/adp0945-xieA.pdf
• https://www.kdd.org/kdd2016/papers/files/adp0945-xieA.pdf
• https://booking.ai/how-booking-com-increases-the-power-of-online-experiments-with-cuped-995d186fff1d
• https://www.tripadvisor.com/engineering/reducing-a-b-test-measurement-variance-by-30/
• https://medium.com/bbc-data-science/increasing-experiment-sensitivity-through-pre-experiment-variance-reduction-166d7d00d8fd
• https://doordash.engineering/2020/06/08/improving-experimental-power-through-control-using-predictions-as-covariate-cupac/
• https://codeascraft.com/2021/06/02/increasing-experimentation-accuracy-and-speed-by-using-control-variates/
• https://dl.acm.org/doi/10.1145/3391403.3399542
• https://www.youtube.com/watch?v=kgIwougeN0M
• https://www.kdd.org/kdd2016/papers/files/adf0653-poyarkovA.pdf
• https://arxiv.org/abs/2106.07263

喜欢就关注一下吧：

点个 在看 你最好看！********** **********