🎈 作者:Linux猿
🎈 简介:CSDN博客专家🏆,华为云享专家🏆,Linux、C/C++、云计算、物联网、面试、刷题、算法尽管咨询我,关注我,有问题私聊!
🎈 关注专栏:数据结构和算法成神路【精讲】优质好文持续更新中……🚀🚀🚀
本篇文章来讲解下大家非常熟悉的一种数据结构-「图」,在算法中使用率非常高,而且,在日常生活中也非常常见,比如:地铁线路图,学校教学楼线路图等。下面赶紧来看一下吧!
🍓一、什么是图?
「图」是一种抽象数据类型,是顶点与其相连的边的集合,图中包含两种数据元素:「顶点」和「边」。下面来看两个简单的图。
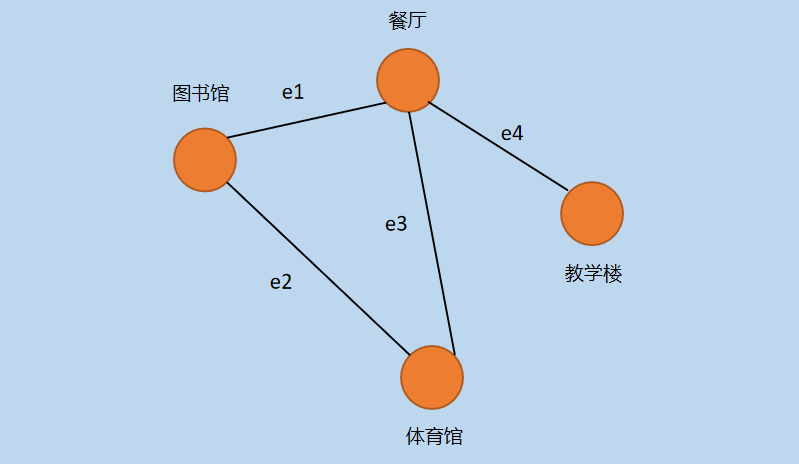
图1 简单无向图
在上图中,〔图书馆〕,〔餐厅〕,〔教学楼〕,〔体育馆〕称为图的「顶点」,通常用大写字母 V 表示顶点的集合,〔餐厅-图书馆〕,〔餐厅-教学楼〕,〔餐厅-体育馆〕,〔图书馆-体育馆〕之间的连线称为「边(或弧)」,一般用大写字母 E 表示边的集合。上图中的边没有方向(边没有方向之分,两端的顶点能够通过同一条边相互到达),称为「无向图」。
下面再来看一个简单「有向图」,如下图所示。
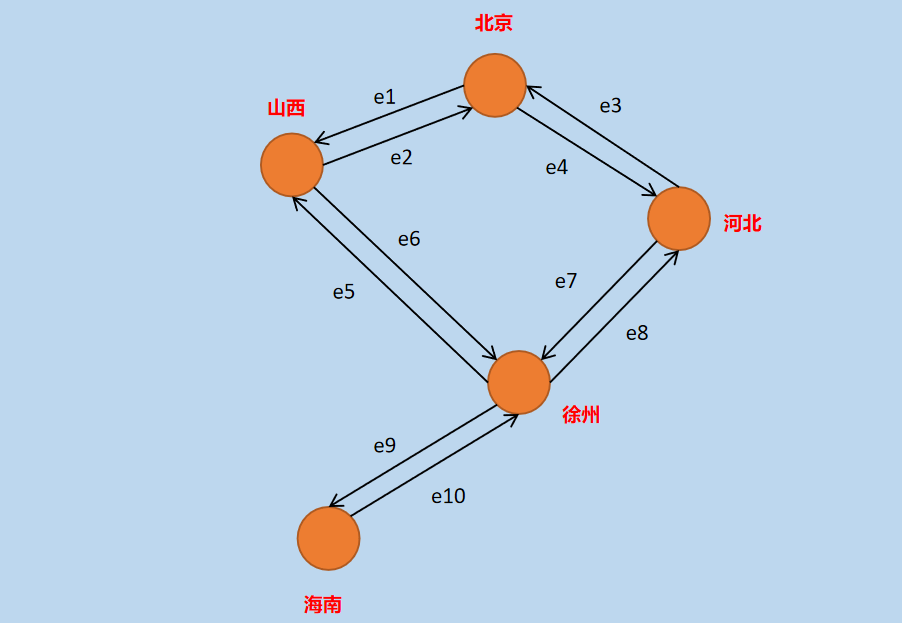
图2 简单有向图
在上图中,顶点为V = {北京、山西、河北、河南、海南} ,边为 E = { e1, e2, e3, e4, e5, e6, e7, e8, e9, e10}。但是,上图中边不同于 「图1」中的边,上图中的边是有方向的,例如:从顶点〔北京〕通过边 「e1」和 「e4」可以直达〔山西〕和〔河北〕,从〔山西〕通过有向边 「e6 」可以直达〔徐州〕,但是,通过「e6 」不能从〔徐州〕到达故〔山西〕,称为「有向图」****。
其中,图边 ei 也称为「弧」,弧的起始顶点称为「弧头」,终点称为「弧尾」****,例如:边 e1,弧尾是顶点北京这一端,弧头是山西这一端。
「有向图」或「无向图」的边通常是有一定含义的,比如:距离、时间、费用等。
好了,大家现在对图有一定理解了,接下来看一下图的特性。
🍅1.1 图的特性
🍎1.1.1 度
顶点 v 的「度」是指与顶点 v 相连的边的〔数量〕。

图3 简单无向图
在上图中,顶点〔餐厅〕的度为 3(与顶点〔餐厅〕相连接的边的〔数量〕为 3),顶点〔图书馆〕的度为 2 (与〔图书馆〕相连的边的〔数量〕为 2)。
🍎1.1.2 出度、入度
「出度」:顶点 v 的出度是指以顶点 v 为尾的弧的〔数量〕;
「入度」:顶点 v 的入度是指以顶点 v 为头的弧的〔数量〕。

图4 出度、入度示意图
在上图中,顶点〔山西〕的出度为 1,入度为1。
🍎1.1.3 邻接点
如果 vi 和 vj 通过边相连,称 vi 和 vj 互为「邻接点」。

图5 邻接点示意图
在上图中,顶点〔北京〕和 〔山西〕互为邻接顶点。
🍎1.1.4 路径、简单路径
「路径」:假设顶点 vi 和 vj 相连通,那么,vi 到 vj 的通路上的顶点的集合称为 vi 到 vj 的一条路径;
「简单路径」:vi 到 vj 的通路上不包含重复的顶点,称 vi 到 vj 的路径为简单路径。
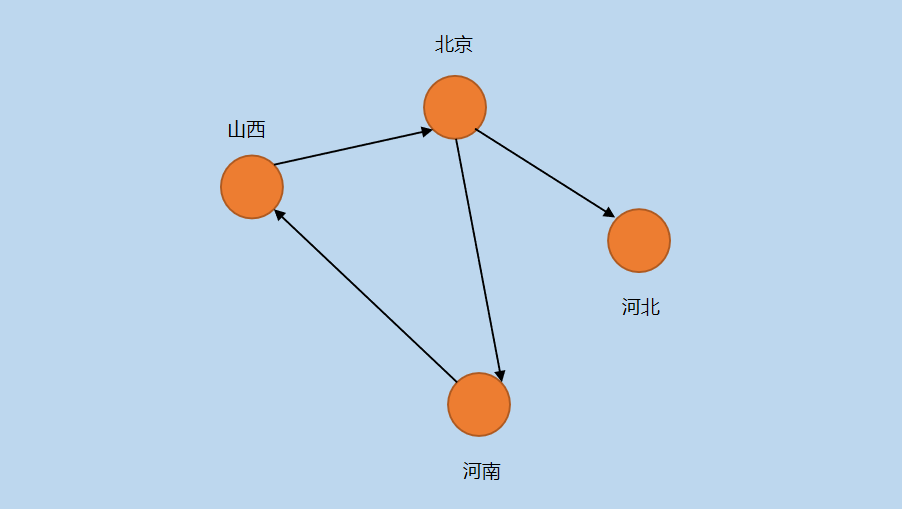
图6 路径示意图
在上图中,〔山西〕 —> 〔北京〕 —> 〔河北〕是一条路径,同样,也是一条「简单路径」,路径上并没有包含重复的顶点。〔北京〕 —> 〔河南〕 —> 〔山西〕 —> 〔北京〕 —> 〔河北〕是一条「路径」,但并不是简单路径,因为包含重复顶点〔北京〕 。
🍎1.1.5 环或回路
「环或回路」:路径的起始点和终点是同一个顶点的路径称为环或回路。

图7 环或回路示意图
在上图中,路径 〔北京〕 —> 〔河南〕 —> 〔山西〕 —> 〔北京〕形成了一个环。
🍎1.1.6 连通图、连通分量
「连通图」和「连通分量」是针对无向图来说的。
在「无向图 G」 中,如果顶点 v 存在一条路径到达顶点 w,则称顶点 v 和 w 是连通的。如果图中任意顶点 vi 和 vj 都是连通的,则称此无向图为「连通图」。
无向图的极大连通子图称为「连通分量」。

图8 无向图 G
在上图无向图 G 中,无向图 G 并不是一个连通图,而其子图 G1 和 G2 都是连通图,G1 和 G2 是图 G 的连通分量。
『 任何连通图的连通分量只有一个,即是其自身,非连通的无向图有多个连通分量。』
🍎1.1.7 强连通图、强连通分量
「强连通图」和「强连通图分量」是针对有向图来说的。
在「有向图 G」中,任意顶点 vi 到 vj 和 vj 到 vi 都存在路径,则称该有向图为「强连通图」。
有向图的极大强连通子图称为「强连通图分量」。
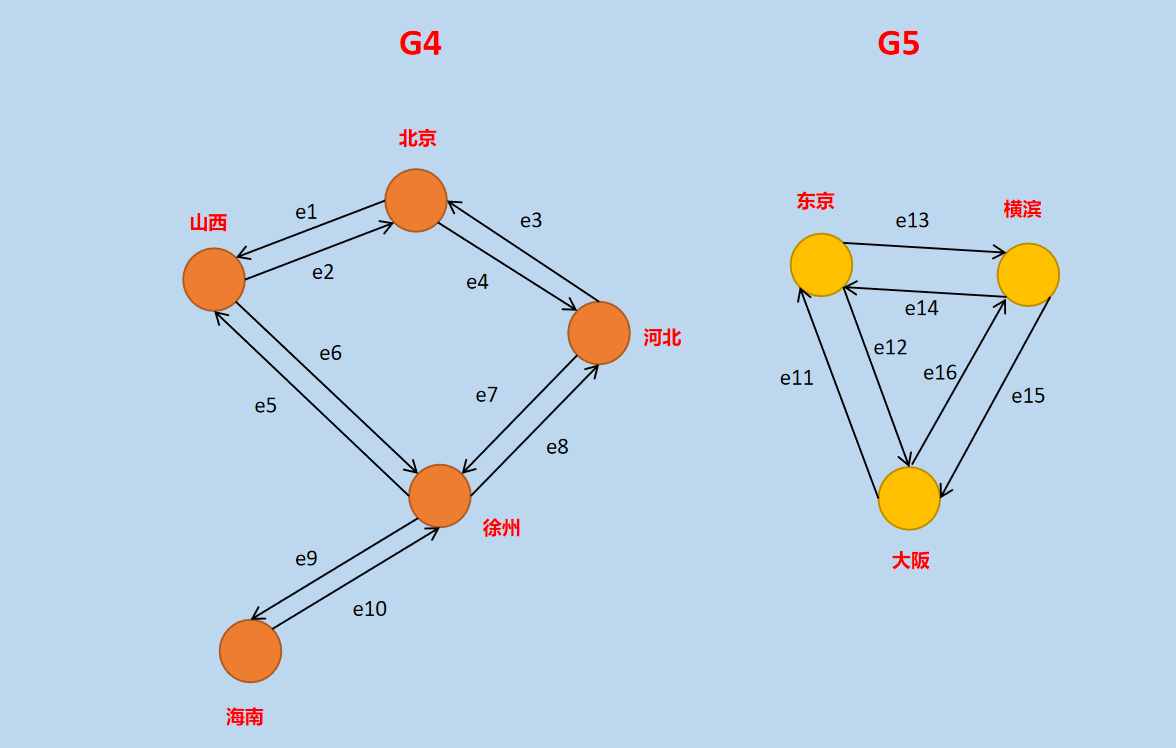
图9 有向图 G3
在上面的「有向图 G3」中,G3 并不是一个强连通图,但是,其包含的 G5 是强连通图,G5 是 G3 的强连通分量,但是,G4 并不是 G3 的强连通分量。
🍅1.2 图的分类
根据不同的分类可以分为不同的图。
🍎1.2.1 有向图和无向图
根据边是否有方向分为:「有向图」和「无向图」。
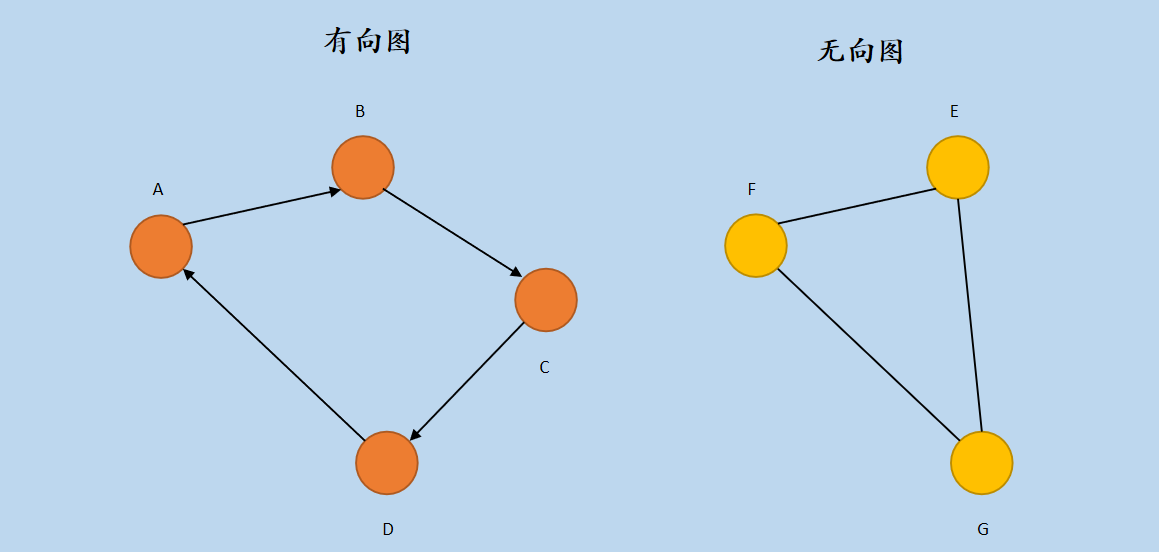
图10 有向图和无向图
在上图中,第一个是「有向图」,边是有方向的,第二个是「无向图」,边是无方向的。
🍎1.2.2 稀疏图和稠密图
根据图的稀疏程度分为:「稀疏图」和「稠密图」。
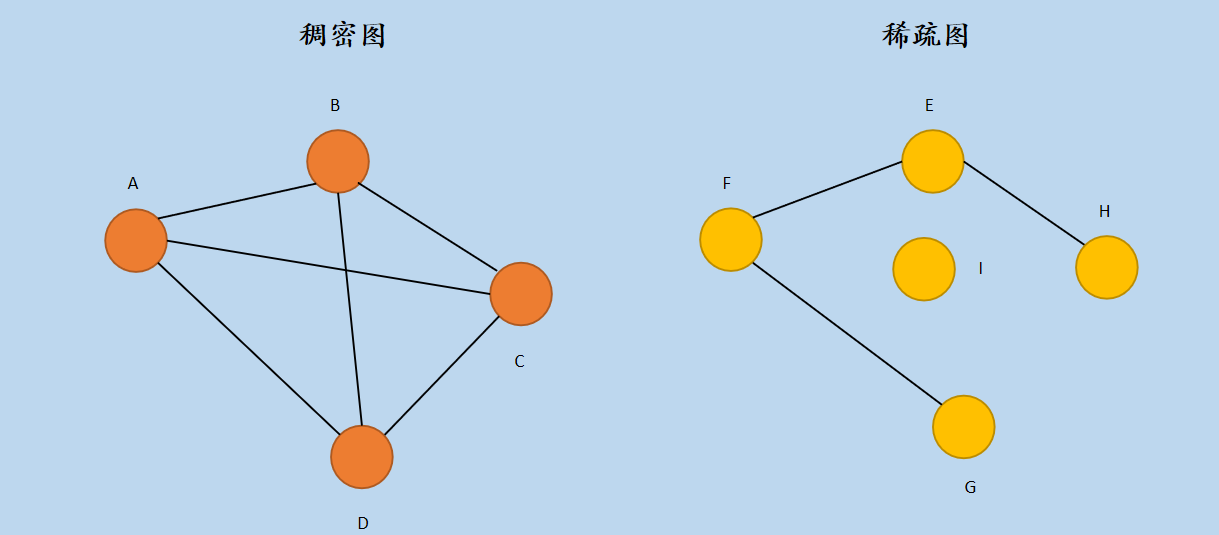
图11 稠密图和稀疏图
在上图中,第一个是「稠密图」,第二个是「稀疏图」,区分条件是通过边的数量来区分,假设 e 为图的边的数量,n 为顶点的数量,那么,满足 e < nlogn 的为「稀疏图」,否则为「稠密图」。有的小伙伴可能有些疑问,为什么要区分「稀疏图」和「稠密图」呢 ?不都是图吗?这些疑问留在下一篇文章中说明。
🍓二、图和树的区别
「图」和「树」都是一种数据结构,但是有如下一些区别。
树中,每个节点最多有一个父亲节点,可以有多个孩子节点,每棵树只有一个根结点,而且都是从根结点出发。
图的概念更广泛,一定形式上,树是具有一定前提条件的图。
🍓三、总结
本篇文章主要对「图」的相关概念进行了详细的介绍,后面的文章将会对「图」的存储进行说明。

🎈 感觉有帮助记得「一键三连****」支持下哦!有问题可在评论区留言💬,感谢大家的一路支持!🤞猿哥将持续输出「优质文章****」回馈大家!🤞🌹🌹🌹🌹🌹🌹🤞

版权归原作者 Linux猿 所有, 如有侵权,请联系我们删除。