冲刺蓝桥31天，第十八天java题解

目录

一、找素数

原题链接

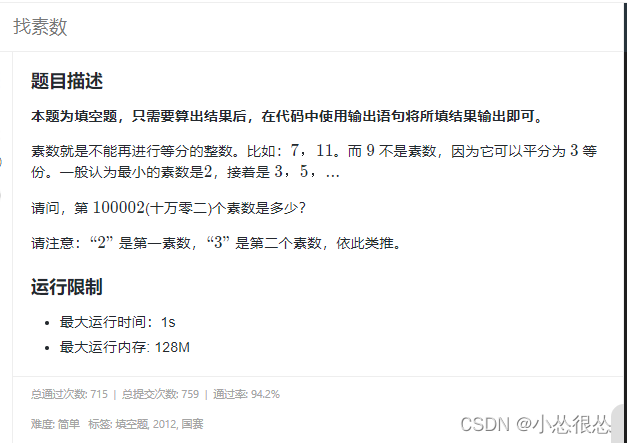
解析：

找素数，这个数没有啥规律可寻找的啊，所以我们选择一个一个进行选择；

因为2/3都是质数，我们从4开始运算好了（因为2/3开方不好搞）；

然后每一次判断是否为质数，是质数就当前质数个数+1，当加到100002时就给它输出

没有到100002就一直往上加就好了，填空题不用怕运行超时，只需要答案即可！

代码：

public class 找素数 {
    public static void main(String[] args) {
        int s=2,t;
        for (int i=4;;i++){
            t= (int) Math.sqrt(i);
            for (int j=2;j<=t;j++){
                if (i%j==0)
                    break;
                else if (j+1>t){
                    s++;
                    if(s==100002){
                        System.out.println(i);
                        return;
                    }
                }
            }
        }
    }
}

二、分考场

原题链接

解析：

这题给定的数值范围在100以内，所以我们选择爆搜，先将认识的两人放在一个数组中

（注意:朋友的朋友不是我的朋友！！！）

所以不能用并查集去排，我们直接用二维数组进行存放

比如 1和3认识，那么 arr[1][3]=1;arr[3][1]=1;说明 1和3互相认识

然后 我们去将每一个考生安排到对应考场

如果一个考生和当前考场的人都不认识，那么可以将他暂时放进该考场

（注意：暂时放入）

因为放入该考场未必是最好的选择，之后我们回溯回来将他再对后面的考场进行查看放入，寻找最优解；

考场使用初始值我们可以设置为一个比较大的数，100个考生最多有100个考场，你初始设置成1000就行，然后每一次判断一下当前使用的考场数量和已经可以到达的最少数量对比，如果比最少数量多，那么就不用继续往下找，直接返回上一次安排；如果当所有学生安排完，你可以获得一个使用的考场数量，而这个数量更小，那就替换当前最小数量，等所有情况分完即结束输出最小数量。

代码：

import java.util.Scanner;

public class 分考场 {

    static int n, min = 100;
    static int[][] arr;//记录关系
    static int[][] brr;//记录考场数量
    static int []crr;//记录每个考场中的人数
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();//n个考试
        int m = sc.nextInt();//m条关系
        arr = new int[n + 1][n + 1];//考生关系
        brr = new int[n + 1][n + 1];//考场数量
        crr = new int[n + 1];//考场人数
        int a, b;
        for (int i = 1; i <= m; i++) {
            a = sc.nextInt();
            b = sc.nextInt();
            arr[a][b] = 1;//记录a，b关系
            arr[b][a] = 1;//相互的
        }
        dfs(1, 0);
        System.out.println(min);
    }
    static void dfs(int x, int y) {
        if (y>= min) return;//如果考场数大于最小考场数，跳过
        if (x> n) {//如果所有学生安排完了,得出最小考场数量
            min = y;
            return;
        }
        //遍历考场数
        for (int i = 1; i <= y; i++) {
            //遍历每个考场的考生人数
            int j;
            for (j = 1; j <= crr[i]; j++) {
                //如果当前考生与本考场中的某位考生认识，跳出
                if(arr[x][brr[i][j]]==1){
                    break;
                }
            }
            //如果当前考生与本考场的人都不认识
            if(j==crr[i]+1){
                //将此考生加入本考场
                brr[i][++crr[i]]=x;
                //dfs继续下一轮搜索
                dfs(x+1,y);
                //回溯
                --crr[i];
            }
        }
        //如果此考生所有考场都有认识的，则开辟一个新的考场
        brr[y+1][++crr[y+1]]=x;
        //dfs继续下一轮搜索
        dfs(x+1,y+1);
        //回溯
        --crr[y+1];
    }
}

三、合根植物

原题链接

解析：

这题主要还是关于并查集吧

（注意：一开始的n,m没什么大的作用，唯一的作用是告诉你总数为n*m）

我们每一次将有关联的数值链接在一起，直接套用并查集模板即可，如果不会，可以套用我代码的，然后去理解一下就行；

（注意：输入的链接关系要运用两次，让所有值关系改成最前面的）

代码：

import java.util.Arrays;
import java.util.Scanner;

public class 合根植物 {
    static Scanner sc=new Scanner(System.in);
    static int m=sc.nextInt();
    static int n=sc.nextInt();
    static int k=sc.nextInt();
    static int[]arr=new int[n*m+1];
    static int [][]brr=new int[k][2];
    public static void main(String[] args) {
        for (int i=1;i<=n*m;i++){
            arr[i]=i;
        }
        for (int i=0;i<k;i++){
            brr[i][0]=sc.nextInt();
            brr[i][1]=sc.nextInt();
            lj(brr[i][0],brr[i][1]);
        }
        for (int i=0;i<k;i++){
            lj(brr[i][0],brr[i][1]);
        }
        int count=0;
        Arrays.sort(arr);
        for (int i=1;i<=n*m;i++){
            if (arr[i]!=arr[i-1]) {
                count++;
            }
        }
        System.out.println(count);
    }
    static void lj(int a,int b){//链接关系
        int arr_a=pd(a),arr_b=pd(b);
        arr[arr_a]=arr_b;
    }
    static int pd(int a){//判断关系
        if (arr[a]==a)
            return a;
        arr[a]=pd(arr[a]);
        return arr[a];
    }
}

四、大胖子走迷宫

原题链接

解析：

这题的起始位置为 3,3 终点位置为 n-2,n-2

我们知道数组下标是从0开始的

所以我们可以更改起始位置是2,2 终点位置是n-3,n-3

这个胖子每一次初始占用的格子为5，所以我们每一次移动需要判断移动后位置5*5范围是否存在障碍点，但是过一段时间他又会变瘦，所以我们要先写好关于变瘦的条件：

我定义的s是时间，k初始值为5，代表重量；
int x = qx.poll(), y = qy.poll();
if (arr[x][y]>=2*s){
    k=1;
}else if (arr[x][y]>=s){
    k=3;
}

判断好了k值的变化，现在来判断每一次需要判断哪些格子，

假设移动到位置 [x][y];然后占用k*k的范围，那么除去当前位置，上下各k/2个格子，左右也各k/2个格子；所以判断代码也可以写出来；我给非"+"初始赋值为-2，“+”赋值为-1，方便计算：

static boolean pd(int x,int y){
    if (x < n-k/2 && x >= k/2 && y < n-k/2 && y >= k/2 && arr[x][y] ==-1){
        for (int i=x-k/2;i<=x+k/2;i++){
            for (int j=y-k/2;j<=y+k/2;j++){
                if (arr[i][j]==-2)
                    return false;
            }
        }
        return true;
    }
    return false;
}

然后题目写了：可以原地不动，那么我们要考虑什么情况下原地不动：

当你上下左右都可以移动的时候，你会往上下左右都移动一步，所以不会原地不动；

当某个方向没有被走过，但是因为太胖了暂时过不去，那么就可以在原地等待变瘦了再过去，所以，在上一个判断之后再添加一次判断，判断是否存在上述情况，存在就将当前位置重新加入队列中，下一次继续判断

（注意：重新加入队列后，当前位置的时间也要更改）

完整代码在下：

代码：

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class 大胖子走迷宫 {
    static Scanner sc = new Scanner(System.in);
    static int n = sc.nextInt();
    static int s = sc.nextInt();
    static int k=5;//定义初始大小
    static int[][] arr = new int[n][n];//位置
    static int ax = 2, ay = 2, bx = n - 3, by = n - 3;//定义初始位置
    public static void main(String[] args) throws Exception {
        init();
        bfs();
    }

    static void init() throws Exception {
        String ss;
        for (int i = 0; i < n; i++) {
            ss = sc.next();
            for (int j = 0; j < ss.length(); j++) {
                if (ss.charAt(j) == '+') {//赋值，方便判断
                    arr[i][j] = -1;
                } else
                    arr[i][j] = -2;
            }
        }
    }

    static void bfs() {
        Queue<Integer> qx = new LinkedList<>();
        Queue<Integer> qy = new LinkedList<>();
        arr[2][2] = 0;//初始位置为0
        qx.add(ax);//加入队列
        qy.add(ay);
        int xa, ya;
        while (!qx.isEmpty()) {//队列非空
            int x = qx.poll(), y = qy.poll();//出列
            if (arr[x][y]>=2*s){//达到这个位置时间为2*s时，体型缩小为1*1
                k=1;
            }else if (arr[x][y]>=s){//达到这个位置时间为s时，体型缩小为3*3
                k=3;
            }
            if (x == bx && y == by) {//达到终点
                System.out.println(arr[bx][by]);
                return;
            }
            for (int i=-1;i<2;i+=2){//左右移动
                xa=x+i;
                if (pd(xa,y)){//判断
                    qx.add(xa);
                    qy.add(y);
                    arr[xa][y]=arr[x][y]+1;
                }
            }
            for (int i=-1;i<2;i+=2){//上下移动
                ya=y+i;
                if (pd(x,ya)){//判断
                    qx.add(x);
                    qy.add(ya);
                    arr[x][ya]=arr[x][y]+1;
                }
            }
            if (x>0&&x<n-1&&y>0&&y<n-1) {//判断是否原地停留
                if (arr[x + 1][y] == -1 || arr[x - 1][y] == -1 || arr[x][y + 1] == -1 || arr[x][y - 1] == -1) {
                    arr[x][y] += 1;//停留增加时间
                    qx.add(x);//重新入列
                    qy.add(y);
                }
            }
        }
    }
    static boolean pd(int x,int y){
        if (x < n-k/2 && x >= k/2 && y < n-k/2 && y >= k/2 && arr[x][y] ==-1){
            for (int i=x-k/2;i<=x+k/2;i++){
                for (int j=y-k/2;j<=y+k/2;j++){
                    if (arr[i][j]==-2)
                        return false;
                }
            }
            return true;
        }
        return false;
    }
}