ctfshow-新手杯
先贴一贴官方wp
国庆放假摆得太厉害，忘记了还有比赛，放完后赶紧回来补一补
crypto4 新手村难度
贴贴题目
from Crypto.Util.number import*from sympy import totient as phi
import sys
import random
defpr(x, end='\n'):
sys.stdout.write(f'{x}{end}')
sys.stdout.flush()defnewbie(naive, p):if(len(naive)==0):return1
NB =1
PH = phi(p)# AAHPHfor i inrange(len(naive)-1,-1,-1):if(NB >4396):# clearlove picked the blind monkreturnpow(naive[0],int(newbie(naive[1:], PH)+ PH),int(p))
NB = naive[i]** NB
return NB % p
BANNER ='''
+-------------------+
| * |
| ** ****** |
| ******** ******* |
| ******** *** |
| * ** *** |
| * *** *** |
| ************* |
| ***************** |
| ** ******* |
| ** *** ** |
| ******** *** ** |
| ** *** ** |
| * **** *** ** |
| ** ** ** ** ** |
| * ** **** ** |
| ** ** *** ** |
| **** ** ** |
| |
+-------------------+
比赛名称：新手杯
比赛时间：2022年10月3日20时，共48小时
比赛类型：个人赛
比赛难度：新手村难度
比赛奖品：神兽抱枕(女用)
题目投稿：[email protected]
投稿奖品：神兽抱枕(男用)
投稿截止：10月1日20时
'''
pr(BANNER)
p = getPrime(64)whileTrue:
p = getPrime(64)if(p %15==2):breakwithopen('flag.txt','rb')as f:
flag = f.read()
flag =f'0{bytes_to_long(flag):b}'
pr(f'{p =}')
pr(f'{len(flag)=}')whileTrue:
pr('> ', end='')
seed =int(input())
random.seed(seed)
newbie_flag =list(flag)
random.shuffle(newbie_flag)
sometimes_naive =[int(x)*2+3for x in newbie_flag]
pr(f'{newbie(sometimes_naive, p)=}')
对照着官方
w
p
wp
wp一顿复现，结果发现
w
p
wp
wp都没怎么看得懂，没想通二次剩余是怎么用的，终究还是我太菜了
先瞅瞅题目整个流程（简化题目，简化问题）
对
f
l
a
g
flag
flag的操作：将
f
l
a
g
flag
flag转成0/1的比特流，然后用
r
a
n
d
o
m
.
s
h
u
f
f
l
e
(
)
random.shuffle()
random.shuffle()打乱顺序，接着将
(
0
,
1
)
(0,1)
(0,1)分别映射到
(
3
,
5
)
(3,5)
(3,5)上，最后丢到
n
e
w
b
i
e
(
)
newbie()
newbie()里面去
再瞧瞧
n
e
w
b
i
e
(
)
newbie()
newbie()函数：不如看
w
p
wp
wp分析，我讲不出什么名堂来，不过可以确定的是
n
e
w
b
i
e
(
)
newbie()
newbie()函数的返回值是
S
0
S
1
S_0^{S_1}
S0S1，看得更简单些就是
3
2
∗
k
+
1
3^{2*k+1}
32∗k+1或
5
2
∗
k
+
1
5^{2*k+1}
52∗k+1
【提示】crypto4 提示为：幂次必为奇数
我自己的想法是既然幂次必为奇数，那么如果
3
2
∗
k
+
1
3^{2*k+1}
32∗k+1或
5
2
∗
k
+
1
5^{2*k+1}
52∗k+1再乘以底数，幂次就变成了偶数（
2
∗
k
+
2
2*k+2
2∗k+2），这样就可以很合理地有限域开方。如果乘
3
3
3以后能开出来那么底就是
3
3
3，那个
b
i
t
bit
bit就为
0
0
0了…这样就求出了第一位的值
利用
s h u f f l e shuffle shuffle来让不同位置的都变成 a 0 a_0 a0来得到所有bit的值
题目需要输入
s
e
e
d
seed
seed，可以控制这样的伪随机，多变变
s
e
e
d
seed
seed来得到所有位置bit的值
先贴贴exp1
p % 4 != 3
会挂掉，要重新跑，懒得写while true try了，将就用吧
拿带pwntools的sage跑，如果sage里面没有pwntools可以分两段，先拿有pwntools的python拿下newbie的值，然后再用sage
#!usr/bin/python3# -*- coding: utf-8 -*-# @Time : 2022/10/8 19:20# @Author : mxx307# @FileName: newbie.py# @Software: PyCharmimport random
import tqdm
from pwn import*from Crypto.Util.number import*
re = remote('pwn.challenge.ctf.show',28104)
tmp = re.recvuntil(b'p = ')
p =int(re.recvline().decode()[:-1])if p %4!=3:
re.close()
exit()
tmp = re.recvuntil(b'len(flag) = ')
flag_len =int(re.recvline().decode()[:-1])print(p,flag_len)# flag_len = 368
flag =[-1for i inrange(flag_len)]# C = []
INDEX =[]
SEED =[]
seed =0whilelen(SEED)!= flag_len:
random.seed(seed)
randlist =list(range(flag_len))
random.shuffle(randlist)
indexx =list(range(flag_len)).index(randlist[0])if indexx notin INDEX:
INDEX.append(indexx)
SEED.append(seed)
seed +=1assertlen(SEED)== flag_len
for i in tqdm.tqdm(range(len(SEED))):
tmp = re.recvuntil(b'> ')
re.sendline(str(SEED[i]).encode())
tmp = re.recvuntil(b'newbie(sometimes_naive, p) = ')
c =int(re.recvline().decode()[:-1])# C.append(c)
PR.<x>= Zmod(int(p))[]
f1 = x * x -3* c
f2 = x * x -5* c
res1 = f1.roots()
res2 = f2.roots()if res1 and res2 ==[]: flag[INDEX[i]]=0elif res1 ==[]and res2: flag[INDEX[i]]=1if flag.count(-1)==0:
flag =[str(i)for i in flag]print(long_to_bytes(int(''.join(flag),2)))break
re.close()# print(f'{C = }')# from Crypto.Util.number import *# flag = [-1 for i in range(flag_len)]# for i in range(len(C)):# c = C[i]# PR.<x> = Zmod(int(p))[]# f1 = x * x - 3 * c# f2 = x * x - 5 * c# res1 = f1.roots()# res2 = f2.roots()# if res1 and res2 == []: flag[INDEX[i]] = 0# elif res1 == [] and res2: flag[INDEX[i]] = 1# if flag.count(-1) == 0:# flag = [str(i) for i in flag]# print(long_to_bytes(int(''.join(flag),2)))# break
写
w
p
wp
wp回过头来思考二次剩余怎么用上去（数论没学好）
根据
w
p
wp
wp，若有
p
≡
3
(
m
o
d
4
)
p\equiv3\ (mod\ 4)
p≡3 (mod 4)，那么
(
3
p
)
=
1
(\frac{3}{p})=1
(p3)=1，即
3
3
3是模
p
p
p的二次剩余。既然
3
3
3是二次剩余，那么
3
k
3^k
3k呢？那必须也得是啊，无论
k
k
k是奇数还是偶数，那么意味着
3
2
∗
k
+
1
3^{2*k+1}
32∗k+1可以被有限域开方求根，但是
5
2
∗
k
+
1
5^{2*k+1}
52∗k+1不行(所以用上面那个exp直接对c开方，能开出来就是3，开不出来就是5，这样也能求，对开方情有独钟)
再想想有没有啥办法不求根就能判断是否为二次剩余呢？
嗯~ o(￣▽￣)o，我想不到，于是
随便找了一篇，看到了Euler判别准则（欧拉准则）
对于奇素数
p
p
p和
p
∤
a
p\nmid a
p∤a（
p
p
p不能被
a
a
a整除）有
a
(
p
−
1
)
/
2
≡
(
a
p
)
≡
{
1
(
m
o
d
p
)
,
若
x
2
≡
a
(
m
o
d
p
)
有解
−
1
(
m
o
d
p
)
,
若
x
2
≡
a
(
m
o
d
p
)
无解
a^{(p-1)/2} \equiv \left(\frac{a}{p}\right) \equiv \left\{\begin{aligned}1\ (mod\ p) ,若x^2\equiv a\ (mod\ p)有解 \\-1\ (mod\ p),若x^2\equiv a\ (mod\ p)无解\end{aligned} \right.
a(p−1)/2≡(pa)≡{1 (mod p),若x2≡a (mod p)有解−1 (mod p),若x2≡a (mod p)无解
判断是否为二次剩余确定是
3
3
3还是
5
5
5
酱紫就简单了些，可能这才是预期解吧（maybe）
最喜欢春哥出的题目辣，每次都能学到很多，这次学到了二次剩余+欧拉准则+高斯二次互反律
春哥yyds
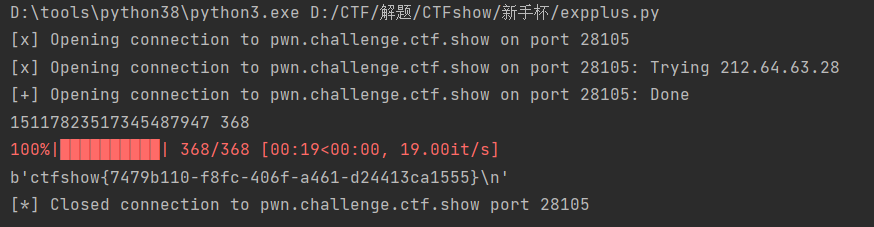
贴贴expplus
p % 4 != 3
会挂掉，要重新跑，懒得写while true try了，将就用吧
#!usr/bin/python3# -*- coding: utf-8 -*-# @Time : 2022/10/9 13:29# @Author : mxx307# @FileName: expplus.py# @Software: PyCharmimport random
import tqdm
from pwn import*from Crypto.Util.number import*
re = remote('pwn.challenge.ctf.show',28105)
re.recvuntil(b'p = ')
p =int(re.recvline().decode()[:-1])if p %4!=3:
re.close()
exit()
re.recvuntil(b'len(flag) = ')
flag_len =int(re.recvline().decode()[:-1])print(p, flag_len)
flag =[-1for i inrange(flag_len)]
INDEX =[]
SEED =[]
seed =0whilelen(SEED)!= flag_len:
random.seed(seed)
randlist =list(range(flag_len))
random.shuffle(randlist)
indexx =list(range(flag_len)).index(randlist[0])if indexx notin INDEX:
INDEX.append(indexx)
SEED.append(seed)
seed +=1assertlen(SEED)== flag_len
for i in tqdm.tqdm(range(len(SEED))):
re.recvuntil(b'> ')
re.sendline(str(SEED[i]).encode())
re.recvuntil(b'newbie(sometimes_naive, p) = ')
c =int(re.recvline().decode()[:-1])
check =pow(c,(p -1)//2, p)
flag[INDEX[i]]=0if check ==1else1
flag =[str(i)for i in flag]print(long_to_bytes(int(''.join(flag),2)))
re.close()
本文转载自: https://blog.csdn.net/qq_53283643/article/details/127225158
版权归原作者 mxx307 所有， 如有侵权，请联系我们删除。
版权归原作者 mxx307 所有， 如有侵权，请联系我们删除。